巡回群
| 代数的構造 → 群論 群論 |
|---|
 |
群論における巡回群(じゅんかいぐん、英: cyclic group、英: monogenous group)とは、ただ一つの元で生成される群(単項生成群)のことである。ここで群が「ただ一つの元で生成される」というのは、その群の適当な元 g をとれば、その群のどの元も(群が乗法的に書かれている場合は)g の整数冪として(群が加法的に書かれている場合は g の整数倍として)表されるということであり、このような元 g はこの群の生成元(generator)あるいは原始元(primitive)と呼ばれる。
定義
[編集]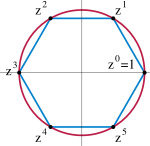
群 G が巡回的(cyclic; 循環的)または巡回群であるとは
となるような元 g ∈ G が存在するときにいう。群の一つの元で生成される群は必ずもとの群の部分群となるから、群 G が巡回群となるかどうかを見るには G の単項生成部分群で G 自身に一致するものがあるかどうかを調べるだけで十分である。
例えば6つの元を持つ集合 G = { g0, g1, g2, g3, g4, g5 } が群となるならば、g6 = g0 であり、G は巡回群を成す。実はこの G は集合 { 0, 1, 2, 3, 4, 5 } に 6 を法とする加法を入れたものに本質的に同じ(つまり同型)である。これは例えば 1 + 2 ≡ 3 (mod 6) に g1 · g2 = g3 が対応し 2 + 5 ≡ 1 (mod 6) に g2 · g5 = g1 が対応するといった具合になっているということを意味する。なんとなれば φ(gi) = i とおくことによりこの同型対応 φ は与えられる。
巡回群は最も簡単な群であり、位数 (order) によりその分類を完全に与えることができる。すなわち、
- 任意の正整数 n に対して、位数が n の巡回群が(同型の違いを除き)ちょうど一つ存在する。
- また、位数が無限大の巡回群が(同型の違いを除き)ちょうど一つ存在する。
「巡回的」という修飾辞がついているので少々紛らわしいところではあるが、生成元 g が無限個の元を生成するというような場合には各 gn は n が異なれば異なるから、(これを無限の長さの循環だということ自体は可能であるのだが)文字通りの意味では巡回しない。このような群は無限巡回群 (infinite cyclic group) と呼ばれ、必ず整数全体の成す加法群 Z に同型になる。さらにいえば、巡回群は必ず(高々)可算(有限または可算無限)個の元しかもたないので(非可算無限個の元をもつ)円周群は巡回群とは「ならない」(円周群は任意の正整数についてそれを位数とする有限巡回群をただひとつ持つので、ある意味で有限巡回群の無限版と看做すことができるものだが、それは無限巡回群ではない)。
任意の巡回群はアーベル群となるので、しばしば加法的に記される。またそのとき、位数 n の巡回群を Zn で表すこともあるが、この記号は数論的な文脈では p-進整数環や素イデアルによる環の局所化の記法と衝突するので問題となりうる。他の標準的な記号としては剰余群の記法に従って Z/nZ, Z/n, Z/(n) などが用いられる。本項ではこれら複数の記法を記号の衝突を避ける目的で使い分けるものとする。後述の巡回群の部分群と記法節も参照のこと。
また、群を乗法的に書く場合には、位数 n の巡回群を Cn で表す(n = ∞ の場合も許す)。例えば g3g4 = g2 は C5 において正しい(このことの加法的な対応物は 「3 + 4 = 2 は Z/5Z において正しい」である)。
性質
[編集]巡回群の基本定理は、「G が位数 n の巡回群ならば G の任意の部分群はそれ自身巡回群であること」、さらには「 G の任意の部分群の位数は n の約数であって、n の各正の約数 k に対して G が位数 k の部分群をちょうど一つ持つこと」[1]を主張するものである。この性質によって有限巡回群が特徴付けられる。すなわち「位数 n の群が巡回群となるための必要十分条件は、n の任意の約数 d に対して位数 d の部分群をちょうど一つ持つこと」[1]である。これは「位数 n の群が巡回群となるための必要十分条件は、n の任意の約数 d に対して位数 d の部分群を高々一つ持つこと」[1]としても同じであり、しばしばこの形で用いられる。
任意の位数 n の有限巡回群は n を法とする加法を備えた群 { [0], [1], [2], ..., [n − 1] } に同型であり、任意の無限巡回群は整数全体の成す集合 Z に加法を考えた加法群 (Z, +) に同型である。したがって、巡回群の性質について理解するには、これらの群だけを調べれば十分である。それゆえ巡回群は調べるのが容易な群の一つであり、巡回群の満たすさまざまな良い性質が知られている。
位数 n の巡回群(n は無限大でもよい)G と G の任意の元 g について、以下のようなことが言える。
- G はアーベル群である[2]。つまり、任意の h ∈ G に対して gh = hg が成り立つ。これは g + h ≡ h + g (mod n) の成立から従う。
- n が有限ならば gn = g0 は群 G の単位元である。これは任意の整数 k に対して kn ≡ 0 (mod n) となることに対応する。
- n = ∞ ならば G はちょうど二つの生成元をもつ。それらは Z における 1 および −1 に対応する元である[3]。
- n が有限ならば G を生成する元の総数はちょうど φ(n) に等しい。ここで φ はオイラーのトーシェント函数である[4]。
- p が素数ならば、位数 p の群は(同型の違いを除き)巡回群 Cp(あるいは加法的に書くならば Z/pZ)しかない[5]。
- 二つの巡回群 Z/nZ, Z/mZ の直積群がふたたび巡回群となるための必要十分条件は n と m が互いに素であることである[6]。従って例えば Z/12Z は Z/3Z と Z/4Z との直積に分解されるが Z/6Z と Z/2Z との直積とはならない。
巡回群の定義から直ちにわかることだが、巡回群は非常に簡素な生成元と基本関係による表示を持つ。すなわち
かつ有限な n に対しては
と書ける。
基本巡回群 とは任意の素数 p と任意の正の整数 k に対して Z/pkZ の形に表される群(素冪位数の群)のことである。有限生成アーベル群の基本定理は、任意の有限生成アーベル群 A が有限個の(有限)基本巡回群と有限個の無限巡回群との直積になることを主張するものである[7]。
Z/nZ および Z は(可換群の構造のみならず)可換環の構造ももつ。p が素数ならば Z/pZ は有限体であり、Fp や GF(p) などとも記される[8]。p 個の元を持つ体は必ずこの Fp に同型となる[8]。環 Z/nZ の単元群は n と互いに素な数の全体からなり、n を法とする乗法のもとで上述の如く位数 φ(n) の乗法群 (Z/nZ)× を成す[4]。例えば、n = 6 として (Z/6Z)× = {1, 5} を、n = 8 として (Z/8Z)× = {1, 3, 5, 7} を得る。
巡回群 Z/nZ の乗法群 (Z/nZ)× がふたたび巡回群となるための必要十分条件は、n が 1, 2, 4 または奇素数 p に対する pk, 2pk (k ≥ 1) の何れかである[9][10][11]。いずれの場合も (Z/nZ)× の生成元を総称して法 n に関する原始根 (primitive root modulo n) という[9][12][13]。したがって (Z/nZ)× は n = 6 のときには巡回群となるが n = 8 のときには巡回群とはならない[14][15](n = 8 のときの (Z/8Z)× はクラインの四元群に同型となる)。特に、n = p が素数ならば (Z/pZ)× は巡回群で p − 1 個の元からなる。これは Z/pZ の 0 でない元の全体とも一致するので、その意味で (Z/pZ)∗ とも書かれる。もっと一般に、任意の斜体の乗法群の有限部分群は必ず巡回群となる(ウェダーバーンの小定理)。特に、任意の有限体の乗法群(および乗法群の部分群)は必ず巡回群となる。巡回群はアーベル群なので任意の有限斜体は(積に関して)可換となる。
例
[編集]二次元および三次元の n 回対称変換の成す対称変換群 Cn は抽象群として Z/nZ に同型である。他にも対称変換群で代数的には同じく巡回群になっているようなものが存在する。
円周上の回転全体の成す群(円周群)S1 は非可算ゆえに巡回群ではないことに注意。
1 の(複素)n 乗根の全体は複素数の乗法に関して位数 n の巡回群を成す。たとえば、n = 3 のとき
であり、{ s0, s1, s2 } は群となるが、これが巡回的なのは見ての通りである。
有限体の任意の有限次拡大のガロワ群は有限巡回群である。逆に、有限体 F と有限巡回群 G が与えられたとき、そのガロワ群が G となるような F の有限次拡大が存在する。
巡回群の表現
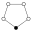
[編集]有限巡回群の巡回グラフはその元の全体を頂点集合とする多角形である。以下の図で、黒点は群の単位元を表し、その他の元は白点で表されている。一つの循環は、単位元(黒点)に連結された頂点(二つあるうちのどちらでもいいから一方)に対応する元の連続する整数冪からなる。
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
巡回群の表現論は、もっと一般の有限群の表現論の重要な基本となる場合となっている。通常表現(複素線型表現)の場合は指標理論と表現論とを透過的に繋ぐことにより、巡回群の表現は(一次)指標の直和に分解される。正標数の場合には、巡回群の直既約表現の全体が、巡回的シロー部分群を持つ群の表現論やもっと一般の blocks of cyclic defect の表現論のモデルおよび帰納的な基礎を成す。
巡回群の部分群と記法
[編集]巡回群の任意の部分群および剰余群は、それ自身が巡回群である。特に整数全体の成す加法群 Z の任意の部分群は、適当な整数 m ≥ 0 によって mZ の形で書ける。これらの部分群は m が異なれば全て互いに異なり、一方(m = 0 のとき自明群となることを除けば)全て Z に同型である。Z の部分群束は整除関係を順序とする自然数全体の成す束の双対に同型である。Z の任意の剰余群は、自明な例外 Z/{0} = Z/0Z を除いて全て有限群である。また n の任意の正の約数 d に対して、剰余群 Z/nZ は位数 d の部分群をちょうど一つ持ち、それは n/d の属する剰余類によって生成される。Z/nZ の部分群は必ずこのようにして得られるので、部分群の束は n の約数全体の成す集合に整除関係で順序を入れたものに同型となる。特に、巡回群が単純群となるための必要十分条件は、その位数(元の個数)が素数となることである。
位数 n の(加法的に書かれた)巡回群を加法群 Z の剰余群として定式化するならば Z/nZ がそれを表す標準的な記法ということになる。あるいは環論の言葉で言えば、部分群 nZ は環 Z のイデアルでもあり、(n) とも書かれるので、同じ巡回群を Z/(n)(あるいは Z/n)と書くことも(剰余環の加法群として捉えれば意味のある記法であるので)記号の濫用ということにはならない。これらの別記法であれば p-進整数環の記法と衝突しないし、後者の記法であれば環としても群としても言葉の上では「Z 割る n」といった感じで読めるので、形式張らない計算ではよく用いられる。
実際の問題としては、g で生成される位数 n の有限部分群 C が与えられたとき、適当な整数 k に対する gk で生成される部分群の位数 m を求めよというようなものが挙げられる。この場合、m は mk が n で割り切れるような最小の正整数として得られるものであり、従って d = gcd(k, n) を k と n の最大公約数とするときの n/d に等しい。別な言い方をすれば gd が生成する部分群の指数が m である。
巡回群の自己準同型
[編集]アーベル群 Z/nZ の自己準同型環は、環としての Z/nZ 自身に同型である。この同型のもとで、数 r は Z/nZ の r 倍写像(各元をその r 個のコピーの和として得られる元に写す自己準同型)に対応する。この自己準同型が全単射となる必要十分条件は r が n と互いに素となることであり、従って Z/nZ の自己同型群は上述の単元群 (Z/nZ)× に同型である。
同様に加法群 Z の自己準同型群は環 Z に同型であり、自己同型群は環 Z の単元群 { ±1 } ≅ C2 に同型である。
実質的巡回群
[編集]群が指数有限な巡回部分群を含むとき、その群を実質的巡回群または実質巡回群と呼び、その群は実質巡回的 (virtually cyclic) であるという。言い換えれば、実質的巡回群の任意の元はその指数有限な巡回部分群の適当な元を掛けることによりある有限集合(完全代表系)の元に写される。
任意の巡回群は実質巡回的であり、同様に任意の有限群も実質巡回的である。また、ちょうど二つの端 (end) を持つ有限生成離散群(例えば Z/nZ と Z の直積群)は実質巡回群となることが知られている。あるいはグロモフの双曲群の任意の可換部分群は実質巡回群となる。
脚注
[編集]- ^ a b c 星 (2016, pp. 94f)
- ^ 星 (2016, pp. 47f)
- ^ 星 (2016, pp. 68–70)
- ^ a b 星 (2016, pp. 77–85)
- ^ 星 (2016, p. 102)
- ^ 星 (2016, p. 123)
- ^ 星 (2016, pp. 129–133)
- ^ a b 星 (2016, pp. 86f)
- ^ a b 星 (2016, pp. 126–129)
- ^ ヴィノグラードフ (1959, pp. 85–98, 第6章 原始根と指数)
- ^ Vinogradov (2003, § VI PRIMITIVE ROOTS AND INDICES)
- ^ ヴィノグラードフ (1959, p. 85)
- ^ Vinogradov (2003, p. 106)
- ^ ヴィノグラードフ (1959, pp. 95–97)
- ^ Vinogradov (2003, pp. 116f)
参考文献
[編集]- 星明考『群論序説』日本評論社、2016年3月25日。ISBN 978-4-535-78809-1。
- Gallian, Joseph (1998) (English), Contemporary abstract algebra (4th ed.), Boston: Houghton Mifflin, ISBN 978-0-669-86179-2, especially chapter 4.
- Herstein, I. N. (1996), Abstract algebra (3rd ed.), Prentice Hall, ISBN 978-0-13-374562-7, MR1375019, especially pages 53–60.
- Vinogradov, I. M. (2003), “§ VI PRIMITIVE ROOTS AND INDICES”, Elements of Number Theory, Mineola, NY: Dover Publications, ISBN 0-486-49530-2
- И.М.ヴィノグラードフ『整数論入門』三瓶与右衛門・山中健 訳、共立出版〈共立全書 517〉、1959年11月。ISBN 978-4-320-00517-4。
- И.М.ヴィノグラードフ『復刊 整数論入門』三瓶与右衛門・山中健 訳、共立出版、2010年2月。ISBN 978-4-320-01917-1。 - ヴィノグラードフ (1959)の復刊。
関連項目
[編集]外部リンク
[編集]- An introduction to cyclic groups
- Weisstein, Eric W. "Cyclic Group". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cyclic Group C_2". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cyclic Group C_3". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cyclic Group C_4". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cyclic Group C_5". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cyclic Group C_6". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cyclic Group C_7". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cyclic Group C_8". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cyclic Group C_9". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cyclic Group C_10". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cyclic Group C_11". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cyclic Group C_12". mathworld.wolfram.com (英語).
- 『巡回群』 - コトバンク