根軸

図 1. 与えられた2つの円（黒）に対する根軸（赤い線）。根軸上の任意の点 P（青）はこの点を中心とし2つの円に直交する固有の円（点線）を持つ。 P を通り各円に接する線分の長さは等しいので、2円に対する方べきも等しくなる。

初等幾何学における2つの円の根軸（こんじく、英: radical axis）とは、2つの円に接線を引いたときその長さが等しくなる点の軌跡である。根軸は2つの円の中心を通る直線に垂直な直線である。2つの円が交わるときには根軸はその交点を通る直線となり、2つの円が接するときには根軸は接点を通る共通接線となる。

根軸上の任意の点 P に対して、P を中心として2円に直交する円が存在する。逆に言えば、2円に直交する円の中心は根軸上にある。他の言い方をすると、根軸上の点 P における2つの円の方べきは等しい、すなわち以下の式が成り立つ。

$R^{2}=d_{1}^{2}-r_{1}^{2}=d_{2}^{2}-r_{2}^{2}$

ここで r₁ と r₂ は2つの円の半径、d₁ と d₂ は P と2つの円の中心との距離であり、R は P を中心として2円に直交する円の半径である。

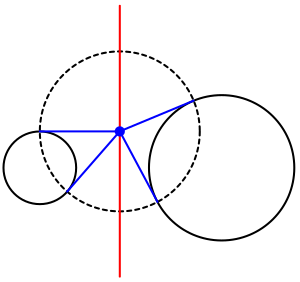
一般的に、2つの離れた円は双極座標系の基底となる。このとき根軸は y軸である。2つの焦点を通る円はy軸上に中心を持ち2つの円に直交するため、その半径は接線の長さに等しいことからy軸が根軸であることがわかる。根軸を共有する円群はアポロニウスの円束と呼ばれる。

定義と性質

2つの円が交わるとき、根軸はその交点を通る割線となる。

図 2. 与えられた3円に直交する円（橙の円）の中心を根心（橙の点）という。

3つの円の根心

どの2つも同心円でない3つの円 A, B, C があるとする。根軸定理とは、3組の円の根軸が1点で交わるかすべて平行であるという定理である。

簡単な証明は以下のとおりである。A と B の根軸上の点から2円に引いた接線の長さは等しい a=b。B と C の根軸上の点においても同様の関係が成り立つ。よってこの2直線の交点では a=b=c が成り立つ。この交点を r とすると a=c が成り立つので A と C の根軸も r を通る。r を根心（radical center）と呼ぶ。

根心を中心として3円に直交する円（根円、radical circle）が存在する。なぜなら、3つの根軸の交点であるためどの2円に対しても直交する円の半径が等しくなるからである。

幾何学的な作図法

根軸の作図法

2つの円 A, B の根軸を作図するためには根軸上の2点がわかればよい。2つの円に交わる円 C を描けば、 A と C の根軸と B と C の根軸は容易に作図できる。この交点を J とすれば上の節の結果より J は根心であり A, B の根軸上にある。同様に2つの円に交わる円 D を描き根心 K を求めれば、J と K を通る直線が求める根軸となる。

図 3. 与えられた2つの円（C と D を中心とする緑と青の円）と相似の中心から引いた線が交わる点を P, Q および S, T とするとこの4点は同一円周上にある。

この作図の特殊な例として図3がある。外部にある2つの円の相似の中心 E をとる。E から2つの円に交わる直線を引き、内側の2つを P, Q とし、同様に S, T をとる。この4点は同一円周上にあるため、P と S を通る直線と Q と T を通る直線の交点は根軸上にある。また、P と Q を通るそれぞれの円の接線を引くと、その交点と P と Q は二等辺三角形となるためこれも根軸上にある。これによって根軸が作図できる。

代数的な作図

図 4. 根軸の位置を計算によって求める。L を J と K の距離とする。x₁ と x₂ を K と B および K と V の距離とする。また、d₁ と d₂ は J と B および J と V の距離とする。

図4によれば、根軸（赤い線）は2つの円の中心 B と V を通る直線（青い線）に垂直である。2つの線の交点 K は B と V の間にある。x₁ と x₂ は K から B と V への距離なので x₁+x₂=D と置くと D は B と V の距離となる。

根軸上に J を取り B と V への距離を d₁, d₂ とすると、方べきの定理より以下が成り立つ。

$d_{1}^{2}-r_{1}^{2}=d_{2}^{2}-r_{2}^{2}$

ここで r₁ と r₂ は2つの円の半径である。ピタゴラスの定理を利用して d₁ と d₂ を x₁, x₂ および J と K の距離 L 置き換えると以下のようになる。

$L^{2}+x_{1}^{2}-r_{1}^{2}=L^{2}+x_{2}^{2}-r_{2}^{2}$

両辺にある L² を消して整理する。

$x_{1}^{2}-x_{2}^{2}=r_{1}^{2}-r_{2}^{2}$

両辺を D = x₁+x₂ で割る。

$x_{1}-x_{2}={\frac {r_{1}^{2}-r_{2}^{2}}{D}}$

両辺に x₁+x₂ = D を足すと x₁ を求める式ができる。

$2x_{1}=D+{\frac {r_{1}^{2}-r_{2}^{2}}{D}}$

同様に x₂ の式も作ることができる。

$2x_{2}=D-{\frac {r_{1}^{2}-r_{2}^{2}}{D}}$

行列による計算

円の式を三線座標で表すと根心の位置を行列式で表すことができる。三角形 ABC 上の点 X を X = x : y : z とし、三辺の長さを a = |BC|, b = |CA|, c = |AB| とする。3つの円は以下の形で表される。

(dx + ey + fz)(ax + by + cz) + g(ayz + bzx + cxy) = 0

(hx + iy + jz)(ax + by + cz) + k(ayz + bzx + cxy) = 0

(lx + my + nz)(ax + by + cz) + p(ayz + bzx + cxy) = 0

この時三円の根心の三線座標は以下の式で表される。

$\det {\begin{bmatrix}g&k&p\\e&i&m\\f&j&n\end{bmatrix}}:\det {\begin{bmatrix}g&k&p\\f&j&n\\d&h&l\end{bmatrix}}:\det {\begin{bmatrix}g&k&p\\d&h&l\\e&i&m\end{bmatrix}}.$

多次元への拡張

3次元空間上の2つの球に対して 同様に根平面（根軸面、根面、radical plane） を定義することができる。これが平面になることは根軸が直線であることと軌跡が2つの球を結ぶ線で対称なことからわかる。

さらに高次元の空間において同様の超平面を定義することができる。

出典

• R. A. Johnson (1960). Advanced Euclidean Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle (reprint of 1929 edition by Houghton Miflin ed.). New York: Dover Publications. pp. 31–43. ISBN 978-0-486-46237-0 
• 鍋島信太郎『幾何学研究』池田書店、1952年。NDLJP:1371532。 
• 長沢亀之助 編、川北朝鄰 閲『初等解析幾何学』数書閣、1892年。NDLJP:828688。 
• 西内貞吉『非ゆうくりつど幾何学』成象堂、1924年。NDLJP:942856。 
• 宮本藤吉『立体解析幾何学 : 高等数学講義』博文館、1911年。NDLJP:828949。 

参考文献

• C. Stanley Ogilvy (1990). Excursions in Geometry. Dover. pp. 17–23. ISBN 0-486-26530-7 
• ハロルド・スコット・マクドナルド・コクセター, S. L. Greitzer (1967). Geometry Revisited. ワシントンD.C.: Mathematical Association of America. pp. 31–36, 160–161. ISBN 978-0-88385-619-2 
• Clark Kimberling, "Triangle Centers and Central Triangles," Congressus Numerantium 129 (1998) i–xxv, 1–295.

外部リンク

• Weisstein, Eric W. "Radical line". mathworld.wolfram.com (英語).
• Weisstein, Eric W. "Chordal theorem". mathworld.wolfram.com (英語).
• Animation at Cut-the-knot