熱場の量子論において松原振動数の和とは、離散的な虚数振動数についての和のこと。松原武生に因んで名付けられた。松原振動数の和は次の形をとる。

ここで は逆温度で、振動数
は逆温度で、振動数 は次の2種類のどちらかである(ただし
は次の2種類のどちらかである(ただし )。
)。
- ボソン振動数:

- フェルミオン振動数:

 が
が の極限で
の極限で よりも速く0に収束するとき、この和は収束する。
ボソン振動数についての和は
よりも速く0に収束するとき、この和は収束する。
ボソン振動数についての和は  (with
(with  )と表され、フェルミオン振動数についての和は
)と表され、フェルミオン振動数についての和は (with
(with  )と表される。ここで
)と表される。ここで は統計的な記号である。
は統計的な記号である。
熱場の量子論に加えて、松原振動数の和は固体物理学における有限温度でのファインマン・ダイアグラムを考える上で重要な役割を果たす[1]。
一般的にファインマン・ダイアグラムは、 では積分
では積分 で表されるが、有限温度では和
で表されるが、有限温度では和 で与えられる。
で与えられる。
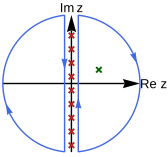 Figure 1.
Figure 1.
 Figure 2.
Figure 2.
松原振動数の和を評価する上手なやり方は、 に極を持つ松原重み関数hη(z)を使う方法である。
ボソンの場合η = +1とフェルミオンの場合η = −1で重み関数は異なる。
重み関数の選択について後述する。
和は、重み関数を使って複素平面での閉曲線積分に置き換えることができる。
に極を持つ松原重み関数hη(z)を使う方法である。
ボソンの場合η = +1とフェルミオンの場合η = −1で重み関数は異なる。
重み関数の選択について後述する。
和は、重み関数を使って複素平面での閉曲線積分に置き換えることができる。

Fig. 1において、重み関数は虚数軸上に極(赤バツ印)を作る。
閉曲線積分はこれらの極の留数をピックアップし、これは和に等しい。
閉曲線をg(z)の極(Fig. 2、緑バツ印)を囲むように変形すると、和はg(z)hη(z)の留数の全ての極g(z)についての和によって形式的に遂行される。

ここで閉曲線が極を時計回りの方向で囲むように変形し、負の留数を生むため、マイナスがつくことに注意。
ボソン振動数 の極を作るために、どちらの半平面で収束がコントロールされるかに依存して次の2つのタイプの松原重み関数を選ぶことができる。
の極を作るために、どちらの半平面で収束がコントロールされるかに依存して次の2つのタイプの松原重み関数を選ぶことができる。


 は左半平面(Re z < 0)での収束をコントロールし、
は左半平面(Re z < 0)での収束をコントロールし、 は右半平面(Re z > 0)での収束をコントロールする。
ここで
は右半平面(Re z > 0)での収束をコントロールする。
ここで はボース分布関数である。
はボース分布関数である。
フェルミオン振動数の場合も同様である。
2つのタイプの松原重み関数があり、 に極を作る。
に極を作る。


 は左半平面(Re z < 0)での収束をコントロールし、
は左半平面(Re z < 0)での収束をコントロールし、 は右半平面(Re z > 0)での収束をコントロールする。
ここで
は右半平面(Re z > 0)での収束をコントロールする。
ここで はフェルミ分布関数である。
はフェルミ分布関数である。
グリーン関数への応用では、g(z)は常に次の構造を持つ。

これは0 < τ < βで与えられる左半平面で発散する。
収束をコントロールするために、第一のタイプの重み関数は常に と選ぶ。
しかし松原振動数の和が発散しないときは収束をコントロールする必要はない。
そのような場合、どんな松原重み関数を選んでも同じ結果が得られる。
と選ぶ。
しかし松原振動数の和が発散しないときは収束をコントロールする必要はない。
そのような場合、どんな松原重み関数を選んでも同じ結果が得られる。
以下の表に、
いくつかの簡単な有理関数g(z)での松原振動数の和をまとめる。

η = ±1 は統計的記号である。

|

|

|
 [1] [1]
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
 [2] [2]
|

|
 [2] [2]
|
[1] 和は収束しないため、松原重み関数の選択が異なると結果は定数分だけ異なる。
[2] (1 ↔ 2)は、手前の項のインデックス1と2を置き換えたものを表す。
極限 での松原振動数の和は、虚数振動数の虚軸についての積分に等しい
での松原振動数の和は、虚数振動数の虚軸についての積分に等しい

いくつかの積分は収束しない。
それらは振動数カットオフ を導入し、
を導入し、 の極限をとる前に積分から発散部分(
の極限をとる前に積分から発散部分( -依存)を差し引いて繰り込む必要がある。
例えば自由エネルギーは、対数の積分によって得られる。
-依存)を差し引いて繰り込む必要がある。
例えば自由エネルギーは、対数の積分によって得られる。
![{\displaystyle \eta \lim _{\Omega \rightarrow \infty }\left[\int _{-i\Omega }^{i\Omega }{\frac {\mathrm {d} (i\omega )}{2\pi }}\left(\ln(-i\omega +\xi )-{\frac {\pi \xi }{2\Omega }}\right)-{\frac {\Omega }{\pi }}(\ln \Omega -1)\right]=\left\{{\begin{array}{cc}0&\xi \geq 0,\\-\eta \xi &\xi <0,\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c939acd61dc3f39c4c14aa6558815b5639264ec)
これは、温度ゼロにおいて自由エネルギーは化学ポテンシャルに満たない内部エネルギーと単純な関係にあることを意味している。
また分布関数は次の積分によって得られる。

これは温度ゼロでの階段関数のふるまいを示している。
虚時間区間(0,β)で定義される関数G(τ)を考える。
これはフーリエ級数の観点で与えられる。

ここで振動数は 2π/β間隔の離散的な値のみとる。
振動数の選択は、関数G(τ)の境界条件に依存している。
物理学ではG(τ)はグリーン関数の虚時間表現を表す。

これはボソン場の周期的境界条件G(τ+β)=G(τ)を満たす。
一方フェルミオン場では、境界条件は反周期的G(τ + β) = −G(τ)である。
振動数領域でのグリーン関数G(iω)が与えられたとき、その虚時間表現G(τ)は松原振動数の和によって評価できる。
その和がボソン振動数かフェルミオン振動数のどちらでとるかに依存して、得られるG(τ)は異なる。
これらを区別するため、次を定義する。



ここでτは区間(0,β)に制限されていることに注意。
境界条件は区間の外にG(τ)を拡張するために用いることができる。
よく用いられる結果を以下の表にまとめる。

|

|

|

|

|

|

|

|

|

|

|

|

|

|
ここでは小さな虚時間が決定的な役割を果たす。
小さな虚時間の負号が変わると、演算子の順番が変わる
 .\
.\
τ = 0でのグリーン関数G(τ)の不連続性のため、分布関数の評価は難しくなる。
次の和を評価するためにボソンとフェルミオンどちらの重み関数を選択することもできるが、結果は異なる。

これは、G(τ)をτ = 0からわずかに遠ざけたとき、収束をコントロールするため、 での重み関数として
での重み関数として をとらなければならず、
をとらなければならず、 では
では をとらなければならないと理解できる。
をとらなければならないと理解できる。
ボソン


フェルミオン


ボソン

フェルミオン

ここでは、よく使われる単一モードのダイアグラムを評価する。
多重モード問題は、スペクトル関数積分によってアプローチできる。



一般的表記 はボース分布関数(η = +1)かフェルミ分布関数(η = −1)のどちらかを表す。
はボース分布関数(η = +1)かフェルミ分布関数(η = −1)のどちらかを表す。

必要であればボース分布関数とフェルミ分布関数を区別するために、それぞれ記号nBとnFを用いる

ボース分布関数は双曲線コタンジェント関数と次の関係にある。

フェルミ分布関数は双曲線タンジェント関数と次の関係にある。

どちらの分布関数も決まったパリティを持っていない。

これは関数 を用いて次のようにも書ける。
を用いて次のようにも書ける。

しかしこれらの導関数は決まったパリティを持つ。
ボース分布関数とフェルミ分布関数は、フェルミオン振動数による変数のシフトの下で変質する。

しかしボソン振動数によるシフトでは違いは生じない。


積で表すと、

温度ゼロの極限では、










定義:

ボソンとフェルミオンでは:



 は正の定関数であることは明らかである。
数値計算でのオーバーフローを避けるため、tanh関数やcoth関数が用いられる。
は正の定関数であることは明らかである。
数値計算でのオーバーフローを避けるため、tanh関数やcoth関数が用いられる。






a = 0において: 
b = 0において: 
一般的に、

- Agustin Nieto: Evaluating Sums over the Matsubara Frequencies. arXiv:hep-ph/9311210
- Github repository: MatsubaraSum A Mathematica package for Matsubara frequency summation.
- ^ A. Abrikosov, L. Gor'kov, I. Dzyaloshinskii: Methods of Quantum Field Theory in Statistical Physics., New York, Dover Publ., 1975, ISBN 0-486-63228-8





































































![{\displaystyle \eta \lim _{\Omega \rightarrow \infty }\left[\int _{-i\Omega }^{i\Omega }{\frac {\mathrm {d} (i\omega )}{2\pi }}\left(\ln(-i\omega +\xi )-{\frac {\pi \xi }{2\Omega }}\right)-{\frac {\Omega }{\pi }}(\ln \Omega -1)\right]=\left\{{\begin{array}{cc}0&\xi \geq 0,\\-\eta \xi &\xi <0,\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c939acd61dc3f39c4c14aa6558815b5639264ec)





































































