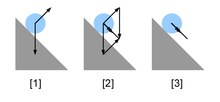
力の平行四辺形 (ちからのへいこうしへんけい、英 : parallelogram of force )は、物体 に2つの力 の加法 によって得られる平行四辺形 である。力の平行四辺形は、2つの力の合力を図示するためにしばしば用いられる。
2つより多くの力のなす図形はもはや平行四辺形ではなくなるが、それらの合力がなす図として同様に平行四辺形を作図できる。例えば、図1 では、F 2 F 1 F 2 F 1 F 2 F 1 , F 2 , G F net = F 1 + F 2 G
図2: 速度の平行四辺形 与えられた時間(例えば1秒 )で粒子 がAからBへの線(図2)に沿って一定の速度で移動し、同時に線ABがABの位置からDCの位置に一様に移動し、終始元の方向と平行なままであるとする。両方の運動を考慮すると、粒子は線ACをたどる。与えられた時間内の変位は速度 の尺度なので、ABの長さはABに沿った粒子の速度の尺度であり、ADの長さはADに沿った線の速度の尺度であり、ACの長さはACに沿った粒子の速度の尺度である。粒子の運動はACに沿って単一の速度で移動した場合と同じである[ 1]
図1の原点(ベクトル の「尾」)にある粒子 に2つの力 が作用したとする。ベクトルF 1 とF 2 の長さは2つの力がある時間作用することにより粒子に生じる速度を表し、それぞれの方向はそれが作用する方向を表している。それぞれの力は独立に作用し、他の力が作用するかしないかにかかわらず特定の速度を作り出す。与えられた時間の終わりでは、粒子は両方の速度を持っている。上記の証明により、これは1つの速度F net と等価である。ニュートンの第2法則 により、このベクトルはその速度を生み出す力の尺度でもあり、したがって、2つの力は1つの力と等価である[ 2]
平行四辺形を用いてなめらかな斜面上の粒子に作用する力を加える。予想通り、結果として生じる力(頭が2つの矢印)が斜面の下向きに作用し、粒子がその方向に加速することが分かる。 力をユークリッドベクトルもしくは
R
2
{\displaystyle \mathbb {R} ^{2}}
F
,
G
∈
R
2
{\displaystyle \mathbf {F} ,\mathbf {G} \in \mathbb {R} ^{2}}
F
⊕
G
∈
R
2
{\displaystyle \mathbf {F} \oplus \mathbf {G} \in \mathbb {R} ^{2}}
R
:
R
2
→
R
2
{\displaystyle R:\mathbb {R} ^{2}\to \mathbb {R} ^{2}}
det
R
=
1
{\displaystyle \det R=1}
R
2
{\displaystyle \mathbb {R} ^{2}}
F
,
G
∈
R
2
{\displaystyle \mathbf {F} ,\mathbf {G} \in \mathbb {R} ^{2}}
R
{\displaystyle R}
R
(
F
⊕
G
)
=
R
(
F
)
⊕
R
(
G
)
{\displaystyle R\left(\mathbf {F} \oplus \mathbf {G} \right)=R\left(\mathbf {F} \right)\oplus R\left(\mathbf {G} \right)}
を満たす。2つの力
F
1
{\displaystyle \mathbf {F} _{1}}
F
2
{\displaystyle \mathbf {F} _{2}}
F
1
{\displaystyle \mathbf {F} _{1}}
a
{\displaystyle a}
F
2
{\displaystyle \mathbf {F} _{2}}
b
{\displaystyle b}
F
1
⊕
F
2
{\displaystyle \mathbf {F} _{1}\oplus \mathbf {F} _{2}}
x
{\displaystyle x}
G
1
:=
a
2
x
2
(
F
1
⊕
F
2
)
{\displaystyle \mathbf {G} _{1}:={\tfrac {a^{2}}{x^{2}}}\left(\mathbf {F} _{1}\oplus \mathbf {F} _{2}\right)}
G
2
:=
a
x
R
(
F
2
)
{\displaystyle \mathbf {G} _{2}:={\tfrac {a}{x}}R(\mathbf {F} _{2})}
R
{\displaystyle R}
F
1
{\displaystyle \mathbf {F} _{1}}
F
1
⊕
F
2
{\displaystyle \mathbf {F} _{1}\oplus \mathbf {F} _{2}}
G
1
=
a
x
R
(
F
1
)
{\displaystyle \mathbf {G_{1}} ={\tfrac {a}{x}}R\left(\mathbf {F} _{1}\right)}
F
1
=
x
a
R
−
1
(
G
1
)
=
a
x
R
−
1
(
F
1
⊕
F
2
)
=
a
x
R
−
1
(
F
1
)
⊕
a
x
R
−
1
(
F
2
)
=
G
1
⊕
G
2
{\displaystyle \mathbf {F} _{1}={\frac {x}{a}}R^{-1}\left(\mathbf {G} _{1}\right)={\frac {a}{x}}R^{-1}\left(\mathbf {F} _{1}\oplus \mathbf {F} _{2}\right)={\frac {a}{x}}R^{-1}\left(\mathbf {F} _{1}\right)\oplus {\frac {a}{x}}R^{-1}\left(\mathbf {F} _{2}\right)=\mathbf {G} _{1}\oplus \mathbf {G} _{2}}
を得る。同様に、さらに2つの力
H
1
:=
−
G
2
,
H
2
:=
b
2
x
2
(
F
1
⊕
F
2
)
{\displaystyle \mathbf {H} _{1}:=-\mathbf {G} _{2},\quad \mathbf {H} _{2}:={\tfrac {b^{2}}{x^{2}}}\left(\mathbf {F} _{1}\oplus \mathbf {F} _{2}\right)}
T
{\displaystyle T}
F
1
{\displaystyle \mathbf {F} _{1}}
H
1
{\displaystyle \mathbf {H} _{1}}
H
1
=
b
x
T
(
F
1
)
{\displaystyle \mathbf {H} _{1}={\tfrac {b}{x}}T\left(\mathbf {F} _{1}\right)}
H
2
=
b
x
T
(
F
2
)
{\displaystyle \mathbf {H} _{2}={\tfrac {b}{x}}T\left(\mathbf {F} _{2}\right)}
F
2
=
x
b
T
−
1
(
H
2
)
=
b
x
T
−
1
(
F
1
⊕
F
2
)
=
b
x
T
−
1
(
F
1
)
⊕
b
x
T
−
1
(
F
2
)
=
H
1
⊕
H
2
{\displaystyle \mathbf {F} _{2}={\frac {x}{b}}T^{-1}\left(\mathbf {H} _{2}\right)={\frac {b}{x}}T^{-1}\left(\mathbf {F} _{1}\oplus \mathbf {F} _{2}\right)={\frac {b}{x}}T^{-1}\left(\mathbf {F} _{1}\right)\oplus {\frac {b}{x}}T^{-1}\left(\mathbf {F} _{2}\right)=\mathbf {H} _{1}\oplus \mathbf {H_{2}} }
これら2つの方程式より
F
1
⊕
F
2
=
(
G
1
⊕
G
2
)
⊕
(
H
1
⊕
H
2
)
=
(
G
1
⊕
G
2
)
⊕
(
−
G
2
⊕
H
2
)
=
G
1
⊕
H
2
{\displaystyle \mathbf {F} _{1}\oplus \mathbf {F} _{2}=\left(\mathbf {G} _{1}\oplus \mathbf {G} _{2}\right)\oplus \left(\mathbf {H} _{1}\oplus \mathbf {H_{2}} \right)=\left(\mathbf {G} _{1}\oplus \mathbf {G} _{2}\right)\oplus \left(-\mathbf {G} _{2}\oplus \mathbf {H} _{2}\right)=\mathbf {G} _{1}\oplus \mathbf {H} _{2}}
を得る。
G
1
{\displaystyle \mathbf {G} _{1}}
H
2
{\displaystyle \mathbf {H} _{2}}
F
1
⊕
F
2
{\displaystyle \mathbf {F} _{1}\oplus \mathbf {F} _{2}}
x
{\displaystyle x}
|
F
1
⊕
F
2
|
=
|
G
1
⊕
H
2
|
=
a
2
x
+
b
2
x
{\displaystyle \left|\mathbf {F} _{1}\oplus \mathbf {F} _{2}\right|=\left|\mathbf {G} _{1}\oplus \mathbf {H} _{2}\right|={\tfrac {a^{2}}{x}}+{\tfrac {b^{2}}{x}}}
x
=
a
2
+
b
2
{\displaystyle x={\sqrt {a^{2}+b^{2}}}}
である。このことは
F
1
⊕
F
2
=
a
e
1
⊕
b
e
2
{\displaystyle \mathbf {F} _{1}\oplus \mathbf {F} _{2}=a\mathbf {e} _{1}\oplus b\mathbf {e} _{2}}
a
2
+
b
2
{\displaystyle {\sqrt {a^{2}+b^{2}}}}
a
e
1
+
b
e
2
{\displaystyle a\mathbf {e} _{1}+b\mathbf {e} _{2}}
F
1
{\displaystyle \mathbf {F} _{1}}
F
2
{\displaystyle \mathbf {F} _{2}}
F
1
⊕
F
2
=
F
1
+
F
2
{\displaystyle \mathbf {F} _{1}\oplus \mathbf {F} _{2}=\mathbf {F} _{1}+\mathbf {F} _{2}}
⊕
{\displaystyle \oplus }
結合性 を用いた。以下の証明にもこの追加の仮定を使用する[ 3] [ 4]
力をユークリッドベクトルもしくは
R
2
{\displaystyle \mathbb {R} ^{2}}
F
,
G
∈
R
2
{\displaystyle \mathbf {F} ,\mathbf {G} \in \mathbb {R} ^{2}}
F
⊕
G
∈
R
2
{\displaystyle \mathbf {F} \oplus \mathbf {G} \in \mathbb {R} ^{2}}
F
⊕
G
=
G
⊕
F
{\displaystyle \mathbf {F} \oplus \mathbf {G} =\mathbf {G} \oplus \mathbf {F} }
写像
(
a
,
b
)
=
a
e
1
+
b
e
2
↦
a
e
1
⊕
b
e
2
{\displaystyle (a,b)=a\mathbf {e} _{1}+b\mathbf {e} _{2}\mapsto a\mathbf {e} _{1}\oplus b\mathbf {e} _{2}}
⊕
{\displaystyle \oplus }
e
1
{\displaystyle \mathbf {e} _{1}}
e
1
{\displaystyle \mathbf {e} _{1}}
e
2
{\displaystyle \mathbf {e} _{2}}
e
2
{\displaystyle \mathbf {e} _{2}}
⊕
{\displaystyle \oplus }
[ 3] [ 5]
力の平行四辺形の数学的証明は、数学的に妥当であると一般に認められていない。さまざまな証明が開発され(主にDuchaylaとポアソン のもの)、これらも反論を引き起こした。力の平行四辺形が真実であるかどうかは疑問視されなかったが、なぜ真実であったのであろうか。今日、力の平行四辺形は経験的事実として受け入れられており、ニュートンの第1原理に還元することはできない[ 3] [ 6]