分子軌道
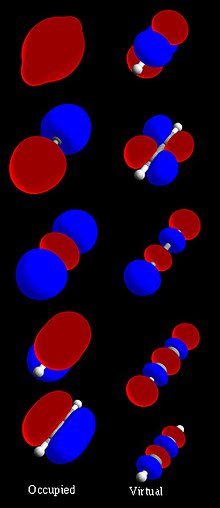

分子軌道(ぶんしきどう)または分子オービタル(英: molecular orbital、略称: MO)は、分子中の各電子の波の様な振る舞いを記述する一電子波動関数のことである。分子軌道法において中心的な役割を果たし、電子に対するシュレーディンガー方程式を、一電子近似を用いて解くことによって得られる。
1個の電子の位置ベクトル の関数であり、 と表される。原子に対する原子軌道に対応するものである。
この関数は、特定の領域に電子を見い出す確率といった化学的、物理学的性質を計算するために使うことができる。「オービタル」(英: orbital)という用語は、「one-electron orbital wave function: 1電子オービタル(軌道〔orbit〕のような)波動関数」の略称として1932年にロバート・マリケンによって導入された[1]。初歩レベルでは、分子軌道は関数が顕著な振幅を持つ空間の「領域」を描写するために使われる。分子軌道は大抵、分子のそれぞれの原子の原子軌道あるいは混成軌道や原子群の分子軌道を結合させて構築される。分子軌道はハートリー-フォック法や自己無撞着場(SCF)法を用いて定量的に計算することができる。
概要
[編集]分子軌道 (MO) は電子が見出される可能性が高い分子中の領域を表わす。分子軌道は、原子中の電子の位置を予測する原子軌道の結合によって得られる。分子軌道は分子の電子配置(一電子〈あるいは電子の対〉の空間的分布ならびにエネルギー)を詳細に記述できる。通常、特に定性的あるいは非常に近似的な利用では、MOは原子軌道の線形結合によって表わされる。これらは分子中の結合の単純なモデルを提供することにおいて非常に有益である。計算化学におけるほとんどの今日的な手法は、系のMOを計算することから始まる。分子軌道は、原子核やその他の電子の平均分布によって生成された電場中の一電子の挙動を記述する。2電子が同じ軌道を占有する場合、パウリの排他原理はそれらが逆のスピンを持つことを要求する。必然的にこれは近似であり、分子の電子波動関数の精度の高い描写は軌道を持たない(配置間相互作用を参照)。
物理的意味
[編集]分子軌道が規格化されているならば、その絶対値の二乗に微小体積を掛けたもの
は、その微小体積中に電子を見出す確率を表す。
応用
[編集]化学反応の理論的予測とその解釈。→フロンティア軌道理論
分子軌道の形成
[編集]分子軌道は原子軌道間の許容された相互作用によって生じる。これは原子軌道の対称性(群論から決定される)が互いに適合する時に許容される。原子軌道相互作用の効率は2つの原子軌道間の重なりによって決定され、これは原子軌道のエネルギーが近接している際に顕著である。最終的に、形成された分子軌道の数は、分子を形成するために結合された原子中の原子軌道の数と等しくなければならない。
定性的議論
[編集]不正確であるが定性的に有用な分子構造の議論のために、分子軌道は「原子軌道の線形結合分子軌道法」アンザッツ(LCAO法)によって得ることができる。ここでは、分子軌道は原子軌道の線形結合として表現される。
原子軌道の線形結合 (LCAO)
[編集]分子軌道は、1927年、1928年にフリードリッヒ・フント[2][3][4][5][6][7] とロバート・マリケン[8][9] によって初めて導入された[10][11]。
原子軌道の線形結合(LCAO)による分子軌道の近似はジョン・レナード=ジョーンズによって1929年に導入された[12]。レナード=ジョーンズの画期的な論文は、量子原理からどのようにしてフッ素および酸素分子の電子構造を導くかを示した。この分子軌道理論への定性的アプローチは現代量子化学の始まりの一部である。
原子軌道の線形結合 (LCAO) は、分子を構成する原子間で結合が起きる際に形成される分子軌道を推定するために使用することができる。原子軌道と同様に、電子の挙動を記述するシュレーディンガー方程式を分子軌道のために構築することができる。原子軌道の線形結合あるいは原子波動関数の和および差は分子のシュレーディンガー方程式の近似解を与える。単純な二原子分子については、得られた波動関数は以下の式で数学的に表現される。
この時、およびはそれぞれ結合性分子軌道および反結合性分子軌道の分子波動関数であり、およびはそれぞれ原子aおよびbの原子波動関数、およびは調整係数である。これらの係数は、個々の原子軌道のエネルギーおよび対称性に依存して、正の値も負の値もとることができる。2つの原子が互いに近接すると、それらの原子軌道は重なり電子密度が高い領域が作られる。その結果、2つの原子間で分子軌道が形成される。原子は、正に荷電した核と結合性分子軌道を占有する負に荷電した電子との間の静電引力によって互いに結び付けられる[13]。
結合性、反結合性、非結合性MO
[編集]原子軌道が相互作用する時、得られた分子軌道には結合性、反結合性あるいは非結合性の3つの種類がある。
- 結合性MO
- 原子軌道間の結合性相互作用は相乗的(同相の)相互作用である。結合性MOはそれらを作るために混合された原子軌道よりもエネルギー的に低い。
- 反結合性MO
- 原子軌道間の反結合性相互作用は相殺的(異相の)相互作用である。反結合性MOはそれらを作るために混合された原子軌道よりもエネルギー的に高い。
- 非結合性MO
- 非結合性MOは適合する対称性の欠如のために原子軌道間で相互作用が起こらなかったことの結果である。非結合性MOは分子中の原子の一つの原子軌道と等しいエネルギーを持つ。
σおよびπ軌道
[編集]原子軌道間の相互作用の種類は、原子軌道の対称性s、pなどと似た分子軌道対称性ラベルσ(シグマ)、π(パイ)などによってさらに分類することができる。
σ対称性
[編集]σ対称性を持つMOは、2つの原子s軌道あるいは2つの原子pz軌道の相互作用によって生じる。軌道が2つの核中心を結ぶ軸(核間軸)に関して対称的とすると、MOはσ対称性を持つ。これは、核間軸の周りのMOの回転が位相を変化させないことを意味する。σ* 軌道(σ反結合性軌道)も、核間軸の周りを回転した時に同じ位相を維持する。σ* 軌道は核の間に核間軸に対して垂直な節面を持つ[14]。
π対称性
[編集]π対称性を持つMOは、2つの原子px軌道あるいはpy軌道の相互作用によって生じる。軌道が核間軸の周りの回転に関して非対称とすると、MOはπ対称性を持つ。これは、核間軸の周りのMOの回転が位相の変化が起きることを意味する。π* 軌道(π反結合性軌道)も、核間軸の周りを回転した時に位相の変化が起きる。π* 軌道もまた核間に節面を持つ[14][15][16][17]。
δ対称性
[編集]δ対称性を持つMOは、2つの原子dxyあるいはdx2-y2軌道の相互作用によって生じる。これらの分子軌道は低エネルギーd原子軌道を含むため、遷移金属錯体中で見られる。
φ対称性
[編集]理論化学者らは、f原子軌道の重なりに対応するφ結合といった高次結合が起こり得ると推測してきた。2005年現在、φ結合を含むと主張されている分子として1例のみが知られている(U2分子中のU−U結合)[18]。
偶対称性および奇対称性
[編集]反転中心を有する分子(中心対称分子)については、分子軌道に対して適応できるさらなる対称性ラベルが存在する。
中心対称分子として以下ものがある。
非中心対称分子としては以下のものがある。
- 異核分子、XY
- 四面体形、EX4
分子中の対称中心を通る反転によって分子軌道の位相が変化しない場合、MOは偶(g、ドイツ語: gerade)対称性を持つと言われる。分子中の対称中心を通る反転によって分子軌道の位相が変化する場合、MOは奇(u、ドイツ語: ungerade)対称性を持つと言われる。
σ対称性を持つ結合性MOでは軌道はσgとラベルでき、σ対称性を持つ反結合性MOでは軌道はσuとラベルできる。π対称性を持つ結合性MOはπuとラベルできる。しかし、π対称性を持つ反結合性MOはπgとラベルできる[14]。
MOダイアグラム
[編集]MOの定性的アプローチは、分子中の結合性相互作用を可視化するために分子軌道ダイアグラムを用いる。このダイアグラムでは、分子軌道は横線で表わされる。高い線の位置は軌道のエネルギーが高いことを表わし、縮退した軌道は間隔を空けて同じ高さに置かれる。次に、分子軌道に対してフントの規則とパウリの排他原理に合うように電子を配置していく。より複雑な分子については、結合の定性的理解において波動力学的アプローチは有用性を失う(しかし定量的アプローチではまだ必要とされる)。
- 軌道の基底関数系は分子軌道相互作用に利用可能な原子軌道(結合性あるいは反結合性)を含む。
- 分子軌道の数は、線形拡張あるいは基底関数系に含まれる原子軌道の数と等しい。
- 分子が対称性を有する場合は、縮退した原子軌道(同じ原子エネルギーを持つ)は線形結合にグループ化される(対称適合原子軌道と呼ばれる)。これは対称変換群の表現に属するため、この群を記述する波動関数は対称適合線形結合 (SALC) として知られている。
- 一つの群表現に属する分子軌道の数は、この表現に属する対称適合原子軌道の数と等しい。
- 特定の表現内では、原子エネルギー準位が近接している場合は対称適合原子軌道はより混合する。
分子軌道における結合
[編集]軌道の縮退
[編集]複数の分子軌道が同じエネルギーを持つ場合、それらは縮退していると言われる。例えば、周期表の最初の10種類の元素の等核二原子分子において、pxおよびpy原子軌道に由来する分子軌道は2つの縮退した結合性軌道(低エネルギー)および2つの縮退した反結合性軌道(高エネルギー)をもたらす[13]。
イオン結合
[編集]2つの原子の原子軌道間のエネルギー差がかなり大きい時、一方の原子の軌道が結合性軌道にほぼ完全に寄与し、もう一方の原子の軌道が反結合性軌道にほぼ完全に寄与する。ゆえに、電子が一方からもう一方の電子に移動した時に、この状況は有効となる。
結合次数および結合長
[編集]分子の結合次数(あるいは結合数)は、結合性および反結合性分子軌道中の電子の数を以下のように組み合わせることで決定することができる。
結合次数 = 0.5*[(結合性軌道中の電子の数) - (反結合性軌道中の電子の数)]
例えば、結合性軌道に8個の電子と反結合性軌道に2つの電子を持つN2の結合次数は3であり、三重結合を構成する。結合長は結合次数に反比例する。
Be2はMOによれば結合次数は0となるが、結合長245 pm、結合エネルギー10 kJ/molの高度に不安定なBe2が存在する実験的証拠があることに留意すべきである[14]。
HOMOおよびLUMO
[編集]最高被占分子軌道(highest occupied molecular orbital)および最低空分子軌道(lowest unoccupied molecular orbital)は、それぞれHOMOおよびLUMOとしばしば呼ばれる。バンドギャップと称されるHOMOおよびLUMOのエネルギー差は、分子の可励起性の指標としての機能を果たす。エネルギー差が小さい程、より励起しやすい。
分子軌道の例
[編集]等核二原子分子
[編集]等核二原子MOは、基底系のそれぞれの原子軌道からの等しい寄与を含んでいる。これはH2、He2、Li2の等核二原子MOダイアグラムで示される(これら全ては対称性軌道を含んでいる)[14]。
H2
[編集]単純なMOの例として、H'、H"とラベルされた2つの原子からなる水素分子H2を考える(分子軌道ダイアグラムを参照)。最低エネルギーの原子軌道1s'および1s"は分子の対称性に応じて変形しない。しかしながら、以下の対称適合原子軌道は変化する。
| 1s' - 1s" | 反対称結合: 鏡映によって変化する、その他の操作では変化しない。 |
|---|---|
| 1s' + 1s" | 対称結合: 全ての対称操作によって変化しない。 |
対称結合(結合性軌道と呼ばれる)は基底軌道よりもエネルギー的に低く、反対称結合(反結合性軌道と呼ばれる)はより高い。H2分子は2つの電子を持つため、それら両方が結合性軌道に入ることができ、2つの自由水素原子よりも系をエネルギー的により低く(つまりより安定に)している。これは共有結合と呼ばれる。「結合次数」は結合性電子の数と反結合性電子の数を足して2で割ったものと等しい。この例では、結合性軌道に2つの電子があり、反結合性軌道には電子がないため結合次数は1となり、2つの水素結合間には単結合が存在する。

He2
[編集]一方、He'、He"とラベルされた原子を持つHe2の仮想的な分子を考えてみる。ここでも、最低エネルギー原子軌道1s'および1s"は分子の対称性に応じて変化しないが、以下の対称適合原子軌道は変化する。
| 1s' - 1s" | 反対称結合: 鏡映によって変化する、その他の操作では変化しない。 |
|---|---|
| 1s' + 1s" | 対称結合: 全ての対称操作によって変化しない。 |
H2分子と同様に、対称結合(結合性軌道と呼ばれる)は基底軌道よりもエネルギー的に低く、反対称結合(反結合性軌道と呼ばれる)はより高い。しかしながら、その基底状態においてそれぞれのヘリウム原子は1s軌道に2つの電子を有しており、合わせると4つの電子がある。2つの電子がより低エネルギーの結合性軌道を占有するが、残りの2つがより高エネルギーの反結合性軌道を占有する。ゆえに、結果として得られた分子の周りの電子密度は2つの電子間の結合(σ結合と呼ばれる)の形成を支持しない。ゆえに、分子は存在しない。もう一つの見方として結合次数を考えると、2つの結合性電子と2つの反結合性電子が存在することから、結合次数は0となり結合は存在しない。
Li2
[編集]二リチウムLi2は2つのLi原子の1sおよび2s原子軌道(基底関数系)の重なりによって形成される。それぞれのLi原子は結合性相互作用に3つの電子を提供し、6つの電子が最低エネルギーにある3つの分子軌道σg(1s)、σu*(1s)、σg(2s)を占有する。結合次数の式を用いると、二リチウムの結合次数は1(単結合)となる。
貴ガス
[編集]He2の仮想的な分子を考えると、原子軌道の基底系がH2の場合と同じであるため、結合性軌道と反結合性軌道がどちらも占有され、エネルギー的な利益はなくなる。HeHはわずかにエネルギー的利益があるがH2 + 2 Heほどではなく、そのため分子は短時間しか存在できない。一般的に、閉殻したHeといった原子はその他の原子とほとんど結合を作らない。短寿命のファンデルワールス錯体を除くと、既知の貴ガス化合物はほとんどない。
異核二原子分子
[編集]等核二原子分子のMOはそれぞれの相互作用する原子軌道から等しい寄与を受けているが、異核二原子分子のMOは異なる原子軌道の寄与を含んでいる。異核二原子分子において、原子軌道の対称性および軌道エネルギーの類似性によって決定される原子軌道間の重なりが十分である場合、結合性あるいは反結合性軌道を作り出すための軌道相互作用が起こる。
HF
[編集]フッ化水素HFにおいて、H 1sおよびF 2s軌道の重なりは対称性によって許容されるが、2つの原子軌道間のエネルギー差が分子軌道を作り出すための相互作用を妨げる。H 1sおよびF 2pz軌道間の重なりも対称性許容であり、これらの2つの原子軌道のエネルギー差は小さい。ゆえに、これらは相互作用し、σおよびσ* MOと結合次数が1の分子が作られる。HFは非中心対称分子であるため、その分子軌道には対称性ラベルgやuは適応されない[19]。
定量的アプローチ
[編集]分子のエネルギー準位の定量的な値を得るため、配置間相互作用 (CI) 拡張がfull CI限界に向かって速く収束するような分子軌道が必要とされる。このような関数を得るための最も一般的な手法が、分子軌道をフォック演算子の固有関数として表現するハートリー-フォック法である。この方法は通常、原子核を中心としたガウス関数の線形結合として分子軌道を表現することによってこの問題を解く。これらの線形結合の係数を求める問題はローターン方程式として知られる一般固有値問題であり、つまりハートリー-フォック方程式の特定の表現である。MOの量子化学計算を行うことができる多くのプログラムがある(例: Spartan、HyperChem)。
単純な説明では、実験的分子軌道エネルギーは原子価軌道に対する紫外光電子分光法と内殻軌道に対するX線光電子分光法によって得ることができることがしばしば示唆される。しかしながら、これらの実験はイオン化エネルギー(分子と1電子を取り除くことで得られるイオンの一つとの間のエネルギー差)を測定しているため不正確である。イオン化エネルギーはクープマンズの定理によって軌道エネルギーと近似的に関連づけられている。これら2つの値がよく一致する分子もあれば、非常に悪い場合もある。
脚注
[編集]- ^ Mulliken, Robert S. (July 1932). “Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations”. Physical Review 41 (1): 49–71. Bibcode: 1932PhRv...41...49M. doi:10.1103/PhysRev.41.49.
- ^ Hund, D. (1926). “Zur Deutung einiger Erscheinungen in den Molekelspektren [On the interpretation of some phenomena in molecular spectra]”. Zeitschrift für Physik 36: 657-674. doi:10.1007/BF01400155.
- ^ Hunt, F. (1927). “Zur Deutung der Molekelspektren. I”. Zeitschrift für Physik 40: 742-764. doi:10.1007/BF01400234.
- ^ Hunt, F. (1927). “Zur Deutung der Molekelspektren. II”. Zeitschrift für Physik 42: 93–120. doi:10.1007/BF01397124.
- ^ Hunt, F. (1927). “Zur Deutung der Molekelspektren. III. Bemerkungen über das Schwingungs- und Rotationsspektrum bei Molekeln mit mehr als zwei Kernen”. Zeitschrift für Physik 43: 805-826. doi:10.1007/BF01397249.
- ^ Hunt, F. (1928). “Zur Deutung der Molekelspektren. IV”. Zeitschrift für Physik 51: 759-795. doi:10.1007/BF01400239.
- ^ Hunt, F. (1930). “Zur Deutung der Molekelspektren V. Die angeregten Elektronenterme von Molekeln mit zwei gleichen Kernen (H2, He2, Li2, N2+, N2 ...)”. Zeitschrift für Physik 63: 719-751. doi:10.1007/BF01339271.
- ^ Mulliken, R. S. (1927). “Electronic States and Band Spectrum Structure in Diatomic Molecules. IV. Hund's Theory; Second Positive Nitrogen and Swan Bands; Alternating Intensities”. Phys. Rev. 29: 637-649. doi:10.1103/PhysRev.29.637.
- ^ Mulliken, R. S. (1928). “The assignment of quantum numbers for electrons in molecules. I”. Phys. Rev. 32: 186-222. doi:10.1103/PhysRev.32.186.
- ^ Werner Kutzelnigg (1996). “Friedrich Hund and Chemistry”. Angew. Chem. Int. Ed. 35: 573-586. doi:10.1002/anie.199605721.
- ^ Mulliken, R. S. (1967). “Spectroscopy, Molecular Orbitals, and Chemical Bonding”. Science 157 (3784): 13-24. doi:10.1126/science.157.3784.13.
- ^ Lennard-Jones, J. E. (1929). “The electronic structure of some diatomic molecules”. Trans. Faraday Soc. 25: 668-686. doi:10.1039/TF9292500668.
- ^ a b Gary L. Miessler; Donald A. Tarr. Inorganic Chemistry. Pearson Prentice Hall, 3rd ed., 2004.
- ^ a b c d e Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.
- ^ Peter Atkins; Julio De Paula. Atkins’ Physical Chemistry. Oxford University Press, 8th ed., 2006.
- ^ Yves Jean; Francois Volatron. An Introduction to Molecular Orbitals. Oxford University Press, 1993.
- ^ Michael Munowitz, Principles of Chemistry, Norton & Company, 2000, p. 229-233.
- ^ Gagliardi, Laura; Roos, Björn O. (2005). “Quantum chemical calculations show that the uranium molecule U2 has a quintuple bond”. Nature 433: 848–851. Bibcode: 2005Natur.433..848G. doi:10.1038/nature03249.
- ^ Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, p. 41-43.
関連項目
[編集]外部リンク
[編集]- Java molecular orbital viewer shows orbitals of hydrogen molecular ion.
- The orbitron, a visualization of all atomic, and some molecular and hybrid orbitals
- xeo Visualizations of some atomic and molecular atoms
- Simulations of molecules with electrons caught in molecular orbital (Simulations run on PC only.)