コンテンツにスキップ

英文维基 | 中文维基 | 日文维基 | 草榴社区

伝送路符号

出典: フリー百科事典『ウィキペディア（Wikipedia）』
（伝送路符号化から転送）

伝送路符号（でんそうろふごう）・ライン符号（line code）は、主にデジタル情報を変換したもので、伝送路や記憶媒体の特性に適した形式で表した符号[1]の総称。電圧・電流・光のパルス波形などの物理信号パターンを構成するのに用いる。

概要

[編集]

伝送路符号では、主にデータとクロックを1つの物理量として同時に生成するための表現方法(セルフクロッキング信号)を扱う。「伝送路」の名称が付いているが、符号化された信号は伝送媒体から送信したりデータ記憶媒体に記録したりすることができる[2][3]。これらの2種類の用途は一見大きく異なって見えるが、同じ方式が使用されるほど特性が類似していることがある。

伝送路符号の物理信号出力では主な用途に以下のものがある。

主な種類

[編集]

基本

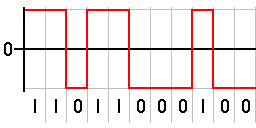
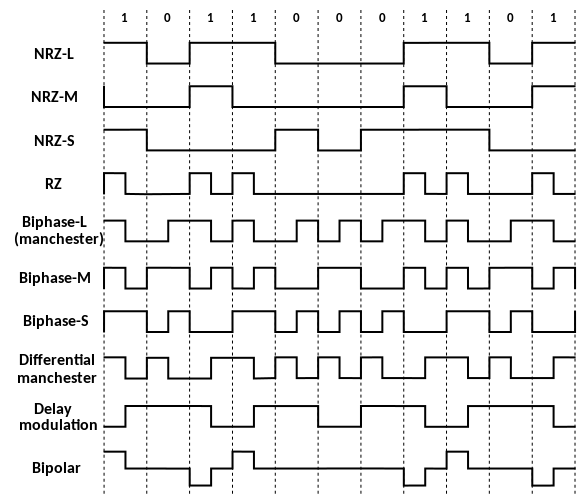
[編集]

ビットと物理信号が1対1対応となる最も基本的な伝送路符号には、次のものがある。

NRZ (1:高, 0:低)
RZ (1:高→ゼロ, 0:低→ゼロ)
マンチェスタ (1:高→低, 0:低→高)
種別 概要 名称 ビット1の表現 ビット0の表現
NRZ "Non-return-to-zero" の略。
信号の高低のみで表現するもの。
最も単純な実装である"Level"と、レベル遷移の有無でビットを表現する"Mark", "Space" (総称 Inverted)の種類がある。 		NRZ-L 高レベルで表す。 低レベルで表す。
NRZ–M
(NRZ-I)		 レベルの遷移で表す。 前のレベルを保つ。
NRZ–S
(NRZ-I)		 前のレベルを保つ。 レベルの遷移で表す。
RZ "Return-to-zero"の略。
正負パルスの後にゼロレベルに復帰するもの。 		RZ ビット周期中の高レベルから0レベルの遷移で表す。 ビット周期中の低レベルから0レベルの遷移で表す。
マンチェスタ符号
(Biphase) 		1ビット周期中に2つの信号レベルがあるもの。
本来のマンチェスタ符号である"Level"と、ビット周期の境界で必ずレベル遷移しながら周期内でのレベル遷移の有無でビットを表現する"Mark", "Space" (差動マンチェスタ符号)などの種類がある。 		Biphase-L ビット周期中の高レベルから低レベルの遷移で表す。 ビット周期中の低レベルから高レベルの遷移で表す。
Biphase-M
(BMC) 		ビット周期中にレベル遷移があることで表す。 ビット周期中にレベル遷移がないことで表す。
Biphase-S ビット周期中にレベル遷移がないことで表す。 ビット周期中にレベル遷移があることで表す。
伝送路符号の実装例[注釈 1][注釈 2][注釈 3][注釈 4]
注釈
  1. ^ ここではRZはユニポーラ(単極)符号として示している (1:高→ゼロ、0:ゼロ)。
  2. ^ 差動マンチェスタ(Differential manchester)は実装の一例として示している (1:エッジ変動あり、0:エッジ変動なし、周期中央で必ず変動)。なお、Biphase-M/Sも差動マンチェスタ符号の1つ。
  3. ^ 遅延符号化(Delay modulation)はMFM符号とも。
  4. ^ バイポーラ(Bipolar)符号は正負・ゼロの3レベルを用いる符号全般を指し、ここでは実装の一例を示している (1:正負レベル交互→ゼロ、0:常にゼロ)。

これらを応用してよく用いられる符号化方式に、次のようなものがある。

マンチェスタの応用

[編集]
名称 概要
差動マンチェスタ符号
1:エッジ変動あり、0:エッジ変動なし、周期中央で必ず変動
マンチェスタ符号の変種で、信号の高低が反転しても同じビット列として復号可能なものを指す。通常のマンチェスタ符号におけるレベル遷移の方向による符号の代わりに、遷移の有無でビットを表す。前述のBiphase-M (BMC)やBiphase-Sなどの方式がある。
MFM符号
上:マンチェスタ(BMC, FM符号)
下:MFM符号
差動マンチェスタ符号(BMC)を改良して、ビット周期の開始値を適宜切り替えて信号変動回数を減らしたもの。フロッピーディスクの記録に用いる。Miller符号化・遅延符号化 (Delay Modulation)とも。
CMI符号（英語版）
"Coded mark inversion"の略。
ビット0は、正負信号を半クロックずつ出力する。正負は前半で直前状態を維持し後半に反転させる。
ビット1は、1クロック分の正負信号いずれかを出力する。正負は直前状態を反転させる[4]。

NRZ, RZの応用

[編集]
名称 概要
AMI符号（英語版）
"Alternate mark inversion"の略。
ビット0はゼロで出力し、ビット1は正負のレベルを交互に出力する[5]。バイポーラ符号の代表的な実装の1つ。
この符号化ではビット0が連続する場合に同期が取れなくなる問題があるため、以下のような改良版が提案されている。ここでは、直前の正負信号と同じ方向のものを「V」、反転方向のものを「B」で表現している。
  • B8ZS: ビット0が8連続する場合に特殊なパターン"000VB0VB"に置き換える。
  • B6ZS: ビット0が6連続する場合に特殊なパターン"0VB0VB"に置き換える。
  • HDB3: ビット0が4連続する場合に特殊なパターン"B00V"または"000V"に置き換える。
  • B3ZS: ビット0が3連続する場合に特殊なパターン"00V"または"B0V"に置き換える。
MLT-3符号
3レベルの出力を負→ゼロ→正→ゼロの順で繰り返し、ビット1=レベル変動、ビット0=レベル維持で表現する。信号変動回数を減らす目的による。
Hybrid Ternary Code（英語版） 以下の変換則に従って正負ゼロの信号を出力するもの[6]。
入力ビット 0 1
直前状態 正 0 負 正 0 負
出力信号 負 負 0 0 正 正
CSRZ（英語版） "Carrier-Suppressed Return-to-Zero"の略。光通信用途。RZを光信号に拡張し、正負レベルを正弦波の±180°位相、ゼロレベルを無点灯で表現する。
APRZ（英語版） "Alternate-Phase Return-to-Zero"の略。光通信用途。上記の位相反転。

異なるビット列への変換

[編集]

連続する0や1(ディスパリティ)が多いビット列を異なるビット列に変換することで物理信号が変動しやすいように調整したもの。多くはNRZを用いた信号として出力される。

名称 概要
4B5B 4ビットのデータを0/1の連続が少ない5ビットに拡張するもの。一般にはFDDIの実装を指す。
6b/8b（英語版） 6ビットのデータを変換し、0/1を4つずつ含む8ビットにするもの。
8b/10b 8ビットを0/1の連続が少ない10ビットに拡張するもの。
64b/66b 64ビットをスクランブル処理し、2ビットの識別子を付加して66ビットに拡張するもの。
128b/130b 128ビットをスクランブル処理し、2ビットの識別子を付加して130ビットに拡張するもの。
EFM変調 8ビットを14ビットに変換する。CDで使用される。
EFMPlus 8ビットを16ビットに変換する。DVDで使用される。
TS-FO-02
(Three of Six, Fiber Optical)		 4ビットのデータを変換し、0/1を3つずつ含む6ビットにするもの。IEEE 1355（英語版）のプラスチックファイバ通信における実装。

複数ビットのパルス化

[編集]

複数のビット列をまとめてパルス出力することで信号周波数低減を図ったもの。多くはパルス振幅変調を用いた信号として出力される。

名称 概要
2B1Q（英語版） 2ビットをPAM4の1シンボルとして出力するもの。特にISDN/HDSLでの実装を指す[7]。
4B3T（英語版） 4ビットのデータを3パルスの正負ゼロ信号(PAM3)として出力するもの。ISDNで用いられる。以下の変換則では、同一ビットに対して複数の出力信号パターンとなるものがいくつかあり、これまでに累積した正負信号の個数が均一になるようなものが選択される[8]。
入力ビット 出力信号 入力ビット 出力信号 入力ビット 出力信号
0000 (=0x0) + 0 + 0110 (=0x6) − + + 1011 (=0xB) + 0 −
0 − 0 − − + 1100 (=0xC) + + +
0001 (=0x1) 0 − + 0111 (=0x7) − 0 + − + −
0010 (=0x2) + − 0 1000 (=0x8) + 0 0 1101 (=0xD) 0 + 0
0011 (=0x3) 0 0 + 0 − − − 0 −
− − 0 1001 (=0x9) + − + 1110 (=0xE) 0 + −
0100 (=0x4) − + 0 − − − 1111 (=0xF) + + 0
0101 (=0x5) 0 + + 1010 (=0xA) + + − 0 0 −
− 0 0 + − −
8B1Q4 8ビットを変換し、PAM5の4シンボルを出力する。特にイーサネットの1000BASE-Tにおける実装を指す。
DSQ128 7ビットを変換し、PAM16の2シンボルを出力する。特にイーサネットの10GBASE-T・5GBASE-T・2.5GBASE-Tにおける実装を指す。
TC-PAM（英語版） 4ビットをトレリス変調し、PAM16の1シンボルを出力する[9]。4B1Hとも。HDSL2やG.SHDSLで使用される。

要件

[編集]

伝送路符号には前述のように多くの方式があり、それぞれ長所と短所がある。一般には次の基準のいずれかを満たすように設計されている。

  • 最小限の伝送回路構成に抑える
  • 同期を容易にする
  • エラー検出と補正を容易にする
  • スペクトル成分(周波数)を最小限に抑える
  • 直流成分(DCバイアス)・ディスパリティを除去・軽減する

ディスパリティ

[編集]

伝送路符号では、一般に連続する0や1の伝送が課題となる。ベースバンド伝送や長距離通信路などでは直流成分(DCバイアス)を確実に伝送できないことが多く、変動しない物理量が続くとエラーが多発する恐れがある。

ビット列中の0と1の個数差をディスパリティ（disparity:不均衡性）と呼び、それまでに送信した全信号のディスパリティの累計をランニングディスパリティ (running disparity) と呼ぶ[10]。これらの軽減のために多くの伝送路符号では同じ物理量が長く連続して出力されないように工夫しており、そのような工夫を直流平衡 (DCバランス, DC-balanced) と呼ぶ。直流平衡には次の3つの方法がある。

  • 定重み符号（英語版）の使用。送信符号は正負信号のそれぞれを十分に含めてその平均レベルがゼロになるように設計されている。実装例として、マンチェスタ符号やITFコードがある。
  • 対ディスパリティ符号（英語版）の使用。この符号化では平均レベルが正の符号と負の符号が対になるように設計されている。送信側では送信中の正負レベルを追跡し、この2種のうち常に正負レベルを0に戻す符号を選択して送る。受信側ではその2種の符号が同じデータビットに復号される。実装例として、AMI符号、8b/10b、4B3Tなどがある。
  • スクランブラの使用。スクランブル回路が生成する擬似乱数により同じ符号の連続が少ないビット列に変換して送付することができる。実装例として、64b/66b（英語版）では RFC 2615 でスクランブラが指定されている。

極性

[編集]

符号化には物理信号に正負の極性として現れるものがあり、以下のように分類される。

バイポーラ符号として最も単純なRZでは正負ゼロの3つの異なる出力レベルがあるため、3の基数を持つ値で解釈される。バイポーラ符号では正負の物理量があるため直流成分を完全に排除できることが主な利点であり、変圧器や長距離伝送路を経由する信号では特に重要となる。

ただし、長距離通信では極性を曖昧にしか読み取れないため、極性に対する検出精度が高くなくとも適切に復号できるような設計が要求され[11][12][13][14]、主に以下の3つの方法がある。

ランレングス制約

[編集]

受信側で精度よくクロック復元するために、生成された符号化列の中で連続する0や1の個数を限定することがある。これを最大ランレングス制約と呼び、主にデータ記憶媒体に適用する符号の特性を表現するときに用いる。

ランレングス制約では、例えば同一符号が最小1個・最大3個の連続に限定される符号化である場合、RLL(1,3)などと記す。連続する同一の符号が長すぎるとクロック復元が困難になり、短すぎると高周波成分の劣化に耐えられない恐れがある。伝送路符号では、符号変動のタイミングをモニタすることでクロック周期が復元されるため、ランレングス制約があることでクロック検出が一定の範囲内に保証される。これにより、最大限にデータを記録・伝送しつつ、 ビット境界の正確な検出が可能となる。このような制約のない場合は読み取り品質を著しく損なう可能性がある。

同期

[編集]
→詳細は「クロック・データ・リカバリ」を参照

伝送路符号は、受信側で受信信号の位相に自身を同期する必要がある。理想的な同期でない場合、符号化で決められた信号レベルを適切に読み取れなくなり、ビット誤り率が増加する。

マンチェスタ符号などのバイフェーズ(biphase)方式では、ビット周期中に少なくとも1つの遷移を必要とするため、送受信機の同期化とエラー検出が容易になるが、信号速度(ボーレート)はNRZ符号よりも高くなる。

エラー検出・訂正

[編集]
→詳細は「誤り検出訂正」を参照

伝送路符号は、物理信号の劣化が受信側でエラーとして処理されるような構造を有することが好ましい。代表的なものとして、パリティビットやCRCなどの付加によるエラー検出や、リード・ソロモン符号やハミング符号などの付加によるエラー訂正を可能とする実装が広く用いられる。

関連項目

[編集]

出典

[編集]
  1. ^ JIS X 0009:1997 情報処理用語（データ通信） 09.05.01
  2. ^ Karl Paulsen. "Coding for Magnetic Storage Mediums".2007.
  3. ^ Abdullatif Glass; Nidhal Abdulaziz; and Eesa Bastaki (2007), “Slope line coding for telecommunication networks”, IEEE International Conference on Signal Processing and Communication (Dubai: IEEE), http://ro.uow.edu.au/cgi/viewcontent.cgi?article=1285&context=dubaipapers, "Line codes ... facilitates the transmission of data over telecommunication and computer networks and its storage in multimedia systems." 
  4. ^ ITU-T G.703 (11/2001), Annex A, A.3. Definition of CMI.
  5. ^ ATIS Telecom Glossary 2000 (28 February 2001). “alternate mark inversion (AMI) signal”. June 9, 2007時点のオリジナルよりアーカイブ。2022年11月1日閲覧。
  6. ^ Glass, A.; Ali, B.; Bastaki, E. (2001). “Design and modeling of H-ternary line encoder for digital data transmission”. Info-tech and Info-net, 2001. Proceedings. ICII 2001 - Beijing (IEEE Xplore) 2: 503–507. doi:10.1109/ICII.2001.983628. ISBN 0-7803-7010-4. 
  7. ^ Whitham D. Reeve (1995). Subscriber Loop Signaling and Transmission Handbook. IEEE Press. ISBN 0780304403. https://archive.org/details/subscriberloopsi00reev 
  8. ^ “Wired Communications T-SMINTO 4B3T Second Gen. Modular ISDN NT (Ordinary)”. Infineon (November 2001). 2022年11月1日閲覧。
  9. ^ Johannes Huber. "Multilevel-Codes: Distance Profiles and Channel Capacity".
  10. ^ Jens Kröger. "Data Transmission at High Rates via Kapton Flexprints for the Mu3e Experiment". 2014. p. 16
  11. ^ Peter E. K. Chow. "Code converter for polarity-insensitive transmission systems". 1983.
  12. ^ David A. Glanzer, Fieldbus Foundation. "Fieldbus Application Guide ... Wiring and Installation". Section "4.7 Polarity". p. 10
  13. ^ George C. Clark Jr., and J. Bibb Cain. "Error-Correction Coding for Digital Communications". 2013. p. 255. quote: "When PSK data modulation is used, the potential exists for an ambiguity in the polarity of the received channel symbols. This problem can be solved in one of two ways. First ... a so-called transparent code. ..."
  14. ^ Prakash C. Gupta. "Data Communications and Computer Networks". 2013. p. 13. quote: "Another benefit of differential encoding is its insensitivity to polarity of the signal. ... If the leads of a twisted pair are accidentally reversed..."

外部リンク

[編集]
「https://ja-two.iwiki.icu/w/index.php?title=伝送路符号&oldid=101645895」から取得