ファブリ・ペロー干渉計による干渉縞。微細構造 が見てとれる。光源 は冷却重水素ランプ (英語版 ) 光学 において、ファブリ・ペロー干渉計 (ファブリ・ペローかんしょうけい、英 : Fabry–Pérot interferometer )もしくはファブリ・ペローのエタロン (英 : etalon ) は、2つの部分反射 面をもつ透明 板や2つの平行 な半透鏡 からなる機器である。その透過 波長 スペクトル は共振 波長に大きな透過率のピークを示す。シャルル・ファブリ とアルフレッド・ペロー に因み命名された[ 1] [ 2] [ 3] [ 4] フランス語 : étalon [ 5]
エタロンは通信 技術やレーザー 技術、分光 技術などにおいて光 の波長を制御・測定するために広く応用されている。近年、技術の進歩により非常に精密に調整されたファブリ・ペロー干渉計の作成が可能となっている。正確には、反射面の間の距離を調整できる構造のものを干渉計 、調節できない構造のものをエタロンと呼ぶ [要出典 が、混同されることが多い。
わずかに楔形をした2つの部分反射板からなるファブリ・ペロー干渉計の模式図。楔角は大きく誇張されており、実際にはゴーストを避けるために数分の一度 程度に抑える必要がある。低フィネスの像と高フィネスの像はそれぞれ反射率 4%(裸ガラス)と 95% に対応する。 ファブリ・ペロー干渉計の心臓部は数マイクロメートル から数センチメートル 離れて向いあう、部分的に光を反射する光学的平面 (英語版 ) ガラス のペアである(または、エタロンの場合は2つの平行な反射面を持つ1枚の板である)。干渉計に使われる平面ガラスは裏面が作る干渉縞 を抑えるために楔形をしていることが多い。また、裏面に無反射コーティング を施すことも多い。
多くの干渉計では、散乱光源をコリメーター レンズ の焦平面 に置く。平面ガラスペアの後ろには、集束レンズを平面ガラスがなかったら光源の反転像が生じるように、つまり光源上のある点から発した全ての光がスクリーン上の一点に集まるように置く。右図には光源上のある点から発する光線を1つだけ赤線で示してある。光線は平面ガラスペアを通過する際に何度も反射されていくつもの光線に分かれ、これらの光線が集束レンズによりスクリーン上の点 A′ に集められる。完全な干渉パターンが生じた際には複数の同心円が現れる。同心円の太さは平面の反射率によって決まる。反射率が高ければQ値 は高くなり、単色光 の場合は細く明るい干渉環が暗い背景に現れる。Q値の高いファブリ・ペロー干渉計は、「フィネス」が高いと表現される。
市販のファブリ・ペロー干渉計 通信分野では光波長多重通信 用のアド・ドロップマルチプレクサ (英語版 ) 石英ガラス またはダイヤモンド 製のエタロンが使われている。これらは mm 玉虫色 の立方体 で、小さな高精度ラックに収められている。材質は温度が変化しても反射面間の距離を一定に維持し、周波数を一定に保つように選ばれる。このため、熱伝導率 が高くかつ熱膨張率 は小さいダイヤモンドが好まれる。2005年 には、エタロンとして機能する光ファイバー を用いる通信機器会社も出てきている。これにより、設置時や冷却に関する手間が大きく削減される。
ダイクロイックフィルタ は光学的平面上に真空蒸着を用いてエタロン層を積層して作られる。このような光学フィルター は吸収フィルターよりも反射帯域および通過帯域が正確であることが多い。カットすべき光を吸収フィルターと違って反射するため、適切に設計すれば温度が上りにくい。ダイクロイックフィルタは光源やカメラ 、天体望遠鏡 、レーザー系などの光学装置に広く用いられている。光波長計 (英語版 ) 光スペクトルアナライザ (英語版 )
レーザー共振器 はしばしばファブリ・ペロー共振器と呼ばれる。しかし多くの場合で片側の反射面の反射率 はほぼ100%であり、ファブリ・ペロー干渉計よりはジル・トルノア干渉計 に近い。半導体ダイオードレーザー には、チップの端面をコーティングすることが難しいために真のファブリ・ペロー構成が用いられることもある。量子カスケードレーザー では活性領域のゲインが高いため、レーザー発振を維持するために端面をコーティングする必要がなく、ファブリ・ペロー共振器が用いられることが多い[ 6] シングルモードレーザーを得るために、レーザー共振器の内部にエタロンを置くことも多い。エタロンが無い場合、一般的にはレーザーはファブリ・ペロー干渉計と似た複数のキャビティ モードに対応する波長域にわたる光を発生させる。ここでレーザーキャビティに慎重に選んだフィネスとフリースペクトル領域のエタロンを挿入すると、一つを除いたキャビティモードを全て抑制することができ、マルチモードレーザーをシングルモードレーザーにすることができる。
ファブリ・ペローのエタロンは、レーザー吸収分光法 (英語版 ) キャビティリングダウン分光法 (英語版 )
ファブリ・ペローのエタロンは通常の分光器 では輝線 が互いに近すぎて観測できないゼーマン効果 をも観測できる分光器として用いられることがある。
天文学 において、エタロンは単一の輝線を選んで撮像 するために用いられる。最もよく用いられる対象は太陽 のHα線 である。太陽のCa-K 線もエタロンを用いて撮像することが多い。重力波 検出器においては、光子 を光速で片道ミリ秒 かかるような長いファブリ・ペローキャビティに貯めることがある。これにより重力波が光と相互作用する時間を長くとることができ、低周波における感度 が向上する。この原理を用いて、LIGO やVirgo干渉計 などの検出器ではマイケルソン干渉計 の両腕を数キロメートル にわたるファブリ・ペローキャビティにより構成している。「クリーナ」と呼ばれるより小さなキャビティもメインレーザーの空間フィルタリング (英語版 ) [ 編集 ] ファブリ・ペロー共振器のスペクトル応答は入射光と共振器内で反射を繰り返す光との干渉 に基いている。これら二つの光の位相 が一致した場合、強めあう干渉が起こり、共振器内の光は増強される。位相が一致していない場合、共振器内に蓄えられるのは入射光の一部のみである。この結果、透過光は入射光に比べてスペクトルが変化している。
幾何学的な距離 ℓ をおいて対向する二枚の鏡の間に、屈折率 n の均一な媒質が満たされているファブリ・ペロー共振器に光が直角に入射するものとする。共振器内の往復時間を t RT c 0 c = c 0 /n Δν FSR は以下のように求められる。
t
RT
=
1
Δ
ν
FSR
=
2
ℓ
c
{\displaystyle t_{\text{RT}}={\frac {1}{\Delta \nu _{\text{FSR}}}}={\frac {2\ell }{c}}}
鏡 i における振幅反射率 r i R i
r
i
2
=
R
i
{\displaystyle r_{i}^{2}=R_{i}}
その他の共振損失はないものとすると、共振器内における光子の減衰時定数 τ c [ 7]
1
τ
c
=
−
ln
(
R
1
R
2
)
t
R
T
{\displaystyle {\frac {1}{\tau _{\mathrm {c} }}}={\frac {-\ln {(R_{1}R_{2})}}{t_{RT}}}}
片道分の位相シフト量を ϕ (ν )ν の光において往復時間 t RT [ 7]
2
ϕ
(
ν
)
=
2
π
ν
t
R
T
.
{\displaystyle 2\phi (\nu )=2\pi \nu t_{RT}.}
共鳴は一往復後の光が強め合う干渉を示す場合に起こる。共鳴モードの指数を正負の整数 q とすると、対応する共鳴周波数 νq および共鳴波数kq について次が成り立つ。
ν
q
=
q
Δ
ν
FSR
⇒
k
q
=
2
π
q
Δ
ν
FSR
c
{\displaystyle \nu _{q}=q\Delta \nu _{\text{FSR}}\Rightarrow k_{q}={\frac {2\pi q\Delta \nu _{\text{FSR}}}{c}}}
符号の反転したモード
±
q
{\displaystyle \pm q}
±
k
{\displaystyle \pm k}
|ν q は同じであるが、光の進行方向が逆であることを示す。
周波数 νq の入射振幅を E q , sτ c フェーザ表示 を用いて次のように表わされる[ 7]
E
q
(
t
)
=
E
q
,
s
e
i
2
π
ν
q
t
e
−
t
2
τ
c
{\displaystyle E_{q}(t)=E_{q,\mathrm {s} }e^{i2\pi \nu _{q}t}e^{-{\frac {t}{2\tau _{c}}}}}
この電場振幅をフーリエ変換 すると、周波数領域における振幅が次のように得られる。
E
~
q
(
ν
)
=
∫
−
∞
+
∞
E
q
(
t
)
e
−
i
2
π
ν
t
d
t
=
E
q
,
s
1
(
2
τ
c
)
−
1
+
i
2
π
(
ν
−
ν
q
)
{\displaystyle {\tilde {E}}_{q}(\nu )=\int _{-\infty }^{+\infty }E_{q}(t)e^{-i2\pi \nu t}\,dt=E_{q,s}{\frac {1}{(2\tau _{c})^{-1}+i2\pi (\nu -\nu _{q})}}}
これを規格化して周波数積分が 1 となるように変換すると、次を得る。
γ
~
q
(
ν
)
=
1
τ
c
|
E
~
q
(
ν
)
E
q
,
s
|
2
=
1
τ
c
1
(
2
τ
c
)
−
2
+
4
π
2
(
ν
−
ν
q
)
2
,
{\displaystyle {\tilde {\gamma }}_{q}(\nu )={\frac {1}{\tau _{c}}}\left|{\frac {{\tilde {E}}_{q}(\nu )}{E_{q,\mathrm {s} }}}\right|^{2}={\frac {1}{\tau _{c}}}{\frac {1}{(2\tau _{c})^{-2}+4\pi ^{2}(\nu -\nu _{q})^{2}}},}
ローレンツィアン スペクトル形状の半値全幅 (FWHM) Δνc を用いると、以下のように書き直せる。
Δ
ν
c
=
1
2
π
τ
c
⇒
γ
~
q
(
ν
)
=
1
π
Δ
ν
c
/
2
(
Δ
ν
c
/
2
)
2
+
(
ν
−
ν
q
)
2
{\displaystyle \Delta \nu _{c}={\frac {1}{2\pi \tau _{c}}}\Rightarrow {\tilde {\gamma }}_{q}(\nu )={\frac {1}{\pi }}{\frac {\Delta \nu _{c}/2}{(\Delta \nu _{c}/2)^{2}+(\nu -\nu _{q})^{2}}}}
ピーク高を 1 となるように規格化すると、次のローレンツィアン線を得る。
γ
q
,
L
(
ν
)
=
π
2
Δ
ν
c
γ
~
q
(
ν
)
=
(
Δ
ν
c
/
2
)
2
(
Δ
ν
c
/
2
)
2
+
4
(
ν
−
ν
q
)
2
.
{\displaystyle \gamma _{q,\mathrm {L} }(\nu )={\frac {\pi }{2}}\Delta \nu _{c}{\tilde {\gamma }}_{q}(\nu )={\frac {(\Delta \nu _{c}/2)^{2}}{(\Delta \nu _{c}/2)^{2}+4(\nu -\nu _{q})^{2}}}.}
全ての q について上記のフーリエ変換を行えば、共振器の完全なモードスペクトルが得られる。
線幅 Δνc と自由スペクトル領域 Δν FSR は周波数に依存しないことから、波長空間では線幅が適切に定義できず、自由スペクトル領域は波長に依存してしまうことから、ファブリ・ペロー共振器の解析は周波数空間で行うのが自然である。
ファブリ・ペロー共振器内の電場振幅[ 7] r 1 , r 1 E inc E refl,1 E laun E circ E b-circ E RT E trans E back E refl E refl,1 E back E laun E RT E refl E trans ファブリ・ペロー共振器の応答を導出するのに最も簡単な方法は循環場アプローチである[ 8]
共振器中を循環する電場 E circ E circ
E
circ
=
E
laun
+
E
RT
=
E
laun
+
r
1
r
2
e
−
i
2
ϕ
E
circ
⇒
E
circ
E
laun
=
1
1
−
r
1
r
2
e
−
i
2
ϕ
{\displaystyle E_{\text{circ}}=E_{\text{laun}}+E_{\text{RT}}=E_{\text{laun}}+r_{1}r_{2}e^{-i2\phi }E_{\text{circ}}\Rightarrow {\frac {E_{\text{circ}}}{E_{\text{laun}}}}={\frac {1}{1-r_{1}r_{2}e^{-i2\phi }}}}
共振器内の光による物理過程のみを考えると、入射光強度と循環光強度との比は一般エアリー分布として次のように導出される[ 7]
A
circ
=
I
circ
I
laun
=
|
E
circ
|
2
|
E
laun
|
2
=
1
|
1
−
r
1
r
2
e
−
i
2
ϕ
|
2
=
1
(
1
−
R
1
R
2
)
2
+
4
R
1
R
2
sin
2
(
ϕ
)
{\displaystyle A_{\text{circ}}={\frac {I_{\text{circ}}}{I_{\text{laun}}}}={\frac {\left|E_{\text{circ}}\right|^{2}}{\left|E_{\text{laun}}\right|^{2}}}={\frac {1}{\left|1-r_{1}r_{2}e^{-i2\phi }\right|^{2}}}={\frac {1}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}}
A circ νq においては sin(ϕ ) = 0 となり、内部共鳴増強因子は次のようになる。
A
circ
(
ν
q
)
=
1
(
1
−
R
1
R
2
)
2
{\displaystyle A_{\text{circ}}(\nu _{q})={\frac {1}{\left(1-{\sqrt {R_{1}R_{2}}}\right)^{2}}}}
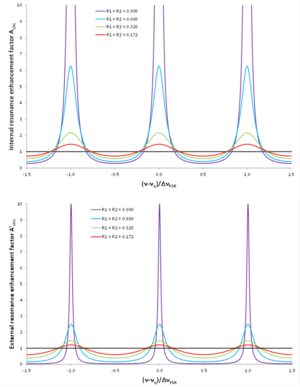
ファブリ・ペロー共振器による共鳴増強[ 7] A circ R 1 = R 2 = 0.9A circ (ν q A ′circ 内部共鳴増強因子、一般エアリー分布が導かれれば、その他のエアリー分布は単純にスケーリング因子により導かれる[ 7]
I
laun
=
(
1
−
R
1
)
I
inc
{\displaystyle I_{\text{laun}}=\left(1-R_{1}\right)I_{\text{inc}}}
そして、鏡 2 の透過光と反射光、および鏡 1 の透過光は共振器内部で循環する光の透過・反射成分であるから、それぞれ次のように書ける。
I
trans
=
(
1
−
R
2
)
I
circ
,
{\displaystyle I_{\text{trans}}=\left(1-R_{2}\right)I_{\text{circ}},}
I
b-circ
=
R
2
I
circ
,
{\displaystyle I_{\text{b-circ}}=R_{2}I_{\text{circ}},}
I
back
=
(
1
−
R
1
)
I
b-circ
{\displaystyle I_{\text{back}}=\left(1-R_{1}\right)I_{\text{b-circ}}}
したがって、共振器内への透過光 I laun A および入射光 I inc A′ は次のように書ける[ 7]
A
circ
=
1
R
2
A
b-circ
=
1
R
1
R
2
A
RT
=
1
1
−
R
2
A
trans
=
1
1
−
R
1
A
back
=
1
1
−
R
1
R
2
A
emit
,
{\displaystyle A_{\text{circ}}={\frac {1}{R_{2}}}A_{\text{b-circ}}={\frac {1}{R_{1}R_{2}}}A_{\text{RT}}={\frac {1}{1-R_{2}}}A_{\text{trans}}={\frac {1}{1-R_{1}}}A_{\text{back}}={\frac {1}{1-R_{1}R_{2}}}A_{\text{emit}},}
A
circ
′
=
1
R
2
A
b-circ
′
=
1
R
1
R
2
A
RT
′
=
1
1
−
R
2
A
trans
′
=
1
1
−
R
1
A
back
′
=
1
1
−
R
1
R
2
A
emit
′
,
{\displaystyle A_{\text{circ}}^{\prime }={\frac {1}{R_{2}}}A_{\text{b-circ}}^{\prime }={\frac {1}{R_{1}R_{2}}}A_{\text{RT}}^{\prime }={\frac {1}{1-R_{2}}}A_{\text{trans}}^{\prime }={\frac {1}{1-R_{1}}}A_{\text{back}}^{\prime }={\frac {1}{1-R_{1}R_{2}}}A_{\text{emit}}^{\prime },}
A
circ
′
=
(
1
−
R
1
)
A
circ
{\displaystyle A_{\text{circ}}^{\prime }=(1-R_{1})A_{\text{circ}}}
下付きの“emit”は共振器の両側から放射される総和強度を考慮したエアリー分布であることを表わす。
後方放射 I back [ 7]
A
refl
′
=
I
refl
I
inc
=
|
E
refl
|
2
|
E
i
n
c
|
2
=
(
R
1
−
R
2
)
2
+
4
R
1
R
2
sin
2
(
ϕ
)
(
1
−
R
1
R
2
)
2
+
4
R
1
R
2
sin
2
(
ϕ
)
{\displaystyle A_{\text{refl}}^{\prime }={\frac {I_{\text{refl}}}{I_{\text{inc}}}}={\frac {\left|E_{\text{refl}}\right|^{2}}{\left|E_{inc}\right|^{2}}}={\frac {\left({{\sqrt {R_{1}}}-{\sqrt {R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}}
いかなる周波数に対しても、どんな干渉があったとしてもエネルギーが保存することはすぐに示すことができる。
A
trans
′
+
A
refl
′
=
I
trans
+
I
refl
I
inc
=
1
{\displaystyle A_{\text{trans}}^{\prime }+A_{\text{refl}}^{\prime }={\frac {I_{\text{trans}}+I_{\text{refl}}}{I_{\text{inc}}}}=1}
外部共鳴増強因子(右図参照)は以下のようになる[ 7]
A
circ
′
=
I
circ
I
i
n
c
=
(
1
−
R
1
)
A
circ
=
1
−
R
1
(
1
−
R
1
R
2
)
2
+
4
R
1
R
2
sin
2
(
ϕ
)
{\displaystyle A_{\text{circ}}^{\prime }={\frac {I_{\text{circ}}}{I_{inc}}}=(1-R_{1})A_{\text{circ}}={\frac {1-R_{1}}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}}
共鳴周波数 νq においては sin(ϕ ) = 0 が成り立つので、以下のように書ける。
A
circ
′
(
ν
q
)
=
1
−
R
1
(
1
−
R
1
R
2
)
2
{\displaystyle A_{\text{circ}}^{\prime }(\nu _{q})={\frac {1-R_{1}}{\left(1-{\sqrt {R_{1}R_{2}}}\right)^{2}}}}
エアリー分布 R 1 = R 2 A ′trans R 1 = R 2 [ 7] ν Airy ν c R 1 = R 2 = 0.9, 0.6, 0.32, 0.172ν Airy /ν c = 1.001, 1.022, 1.132, 1.717 通常、光はファブリ・ペロー共振器を透過する。したがって、よく適用されるエアリー分布は以下のものである[ 7]
A
trans
′
=
I
trans
I
inc
=
(
1
−
R
1
)
(
1
−
R
2
)
A
circ
=
(
1
−
R
1
)
(
1
−
R
2
)
(
1
−
R
1
R
2
)
2
+
4
R
1
R
2
sin
2
(
ϕ
)
{\displaystyle A_{\text{trans}}^{\prime }={\frac {I_{\text{trans}}}{I_{\text{inc}}}}=(1-R_{1})(1-R_{2})A_{\text{circ}}={\frac {(1-R_{1})(1-R_{2})}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}}
これは光源から鏡 1 に入射する光の強度 I inc I trans ν q
A
trans
′
(
ν
q
)
=
(
1
−
R
1
)
(
1
−
R
2
)
(
1
−
R
1
R
2
)
2
{\displaystyle A_{\text{trans}}^{\prime }(\nu _{q})={\frac {(1-R_{1})(1-R_{2})}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}}}}
であり、R 1 = R 2
A ′trans [ 8] e iπ /2
E
circ
=
i
t
1
E
inc
+
r
1
r
2
e
−
i
2
ϕ
E
circ
⇒
E
circ
E
inc
=
i
t
1
1
−
r
1
r
2
e
−
i
2
ϕ
,
{\displaystyle E_{\text{circ}}=it_{1}E_{\text{inc}}+r_{1}r_{2}e^{-i2\phi }E_{\text{circ}}\Rightarrow {\frac {E_{\text{circ}}}{E_{\text{inc}}}}={\frac {it_{1}}{1-r_{1}r_{2}e^{-i2\phi }}},}
E
trans
=
i
t
2
E
circ
e
−
i
ϕ
⇒
E
trans
E
inc
=
−
t
1
t
2
e
−
i
ϕ
1
−
r
1
r
2
e
−
i
2
ϕ
{\displaystyle E_{\text{trans}}=it_{2}E_{\text{circ}}e^{-i\phi }\Rightarrow {\frac {E_{\text{trans}}}{E_{\text{inc}}}}={\frac {-t_{1}t_{2}e^{-i\phi }}{1-r_{1}r_{2}e^{-i2\phi }}}}
A
trans
′
=
I
trans
I
inc
=
|
E
trans
|
2
|
E
inc
|
2
=
|
−
t
1
t
2
e
−
i
ϕ
|
2
|
1
−
r
1
r
2
e
−
i
2
ϕ
|
2
=
(
1
−
R
1
)
(
1
−
R
2
)
(
1
−
R
1
R
2
)
2
+
4
R
1
R
2
sin
2
(
ϕ
)
{\displaystyle A_{\text{trans}}^{\prime }={\frac {I_{\text{trans}}}{I_{\text{inc}}}}={\frac {\left|E_{\text{trans}}\right|^{2}}{\left|E_{\text{inc}}\right|^{2}}}={\frac {\left|-t_{1}t_{2}e^{-i\phi }\right|^{2}}{\left|1-r_{1}r_{2}e^{-i2\phi }\right|^{2}}}={\frac {(1-R_{1})(1-R_{2})}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}}
また、A ′[ 9] E inc E trans 漸化式 で表わせる。
E
trans
,
1
=
E
inc
i
t
1
i
t
2
e
−
i
ϕ
=
−
E
inc
t
1
t
2
e
−
i
ϕ
,
{\displaystyle E_{{\text{trans}},1}=E_{\text{inc}}it_{1}it_{2}e^{-i\phi }=-E_{\text{inc}}t_{1}t_{2}e^{-i\phi },}
E
trans
,
m
+
1
=
E
trans
,
m
r
1
r
2
e
−
i
2
ϕ
{\displaystyle E_{{\text{trans}},m+1}=E_{{\text{trans}},m}r_{1}r_{2}e^{-i2\phi }}
これを足し合わせるとこのようになる。
∑
m
=
0
∞
x
m
=
1
1
−
x
⇒
E
trans
=
∑
m
=
1
∞
E
trans
,
m
=
E
i
n
c
−
t
1
t
2
e
−
i
ϕ
1
−
r
1
r
2
e
−
i
2
ϕ
{\displaystyle \sum _{m=0}^{\infty }x^{m}={\frac {1}{1-x}}\Rightarrow E_{\text{trans}}=\sum _{m=1}^{\infty }E_{{\text{trans}},m}=E_{inc}{\frac {-t_{1}t_{2}e^{-i\phi }}{1-r_{1}r_{2}e^{-i2\phi }}}}
したがって E trans / E inc A ′
[ 編集 ] 物理的には、エアリー分布は共振器の縦モードの和である[ 7] E circ ~ γ q ν )t RT
γ
q
,
emit
(
ν
)
=
1
t
RT
γ
~
q
(
ν
)
{\displaystyle \gamma _{q,{\text{emit}}}(\nu )={\frac {1}{t_{\text{RT}}}}{\tilde {\gamma }}_{q}(\nu )}
これを全ての縦モードについて総和をとると、[ 7]
∑
q
=
−
∞
∞
γ
q
,
emit
(
ν
)
=
1
−
R
1
R
2
(
1
−
R
1
R
2
)
2
+
4
R
1
R
2
sin
2
(
ϕ
)
=
A
emit
{\displaystyle \sum _{q=-\infty }^{\infty }\gamma _{q,{\text{emit}}}(\nu )={\frac {1-R_{1}R_{2}}{\left({1-{\sqrt {R_{1}R_{2}}}}\right)^{2}+4{\sqrt {R_{1}R_{2}}}\sin ^{2}(\phi )}}=A_{\text{emit}}}
となり、エアリー分布 A emit
単純なスケーリング因子により、個々のエアリー分布と γ q , emit[ 7]
γ
q
,
circ
=
1
R
2
γ
q
,
b-circ
=
1
R
1
R
2
γ
q
,
RT
=
1
1
−
R
2
γ
q
,
trans
=
1
1
−
R
1
γ
q
,
back
=
1
1
−
R
1
R
2
γ
q
,
emit
,
{\displaystyle \gamma _{q,{\text{circ}}}={\frac {1}{R_{2}}}\gamma _{q,{\text{b-circ}}}={\frac {1}{R_{1}R_{2}}}\gamma _{q,{\text{RT}}}={\frac {1}{1-R_{2}}}\gamma _{q,{\text{trans}}}={\frac {1}{1-R_{1}}}\gamma _{q,{\text{back}}}={\frac {1}{1-R_{1}R_{2}}}\gamma _{q,{\text{emit}}},}
γ
q
,
circ
′
=
1
R
2
γ
q
,
b-circ
′
=
1
R
1
R
2
γ
q
,
RT
′
=
1
1
−
R
2
γ
q
,
trans
′
=
1
1
−
R
1
γ
q
,
back
′
=
1
1
−
R
1
R
2
γ
q
,
emit
′
,
{\displaystyle \gamma _{q,{\text{circ}}}^{\prime }={\frac {1}{R_{2}}}\gamma _{q,{\text{b-circ}}}^{\prime }={\frac {1}{R_{1}R_{2}}}\gamma _{q,{\text{RT}}}^{\prime }={\frac {1}{1-R_{2}}}\gamma _{q,{\text{trans}}}^{\prime }={\frac {1}{1-R_{1}}}\gamma _{q,{\text{back}}}^{\prime }={\frac {1}{1-R_{1}R_{2}}}\gamma _{q,{\text{emit}}}^{\prime },}
γ
q
,
circ
′
=
(
1
−
R
1
)
γ
q
,
circ
{\displaystyle \gamma _{q,{\text{circ}}}^{\prime }=(1-R_{1})\gamma _{q,{\text{circ}}}}
[ 編集 ] スペクトル分解能に関するテイラーの基準では、個々のピークが半値において交われば分解能があるとする。光がファブリ・ペロー共振器内へ透過するとき、エアリー分布を計測するとファブリ・ペロー共振器の総損失をローレンツィアン線幅 Δν c (下図青線)と自由スペクトル領域との比を再計算することにより計算することができる。
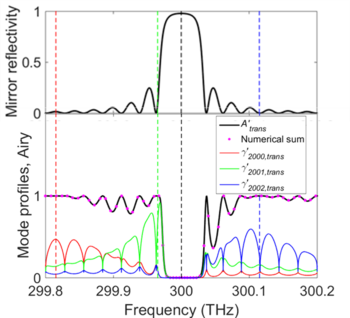
ファブリ・ペロー共振器におけるローレンツィアン線幅とフィネス、およびエアリー線幅とフィネスの関係[ 7] Δν c / Δν FSR (青線)および相対エアリー線幅 Δν Airy / Δν FSR (緑線)とその近似式(赤線)。右図: ローレンツィアンフィネス ℱc (青線)および、エアリーフィネス ℱAiry (緑線)とその近似式(赤線)。どちらも横軸は反射率 R 1 R 2 Δν Airy = Δν FSR 、すなわち ℱAiry = 1 において定義されなくなるが、近似解(赤線)は崩壊しない。インセットは領域 R 1 R 2 < 0.1 ファブリ・ペロー共振器のローレンツィアンフィネス ℱc の物理的な意味[ 7] R 1 = R 2 ≈ 4.32%Δν c = Δν FSR および ℱAiry = 1 が成り立ち、隣接するローレンツィアンピーク(破線、図の見易さのため5つのみ表示)同士が半値(黒線)において交わり、エアリー分布(紫実線)二つのピークの分解能に関するテイラーの基準が成り立つ際を表示してある。 ローレンツィアンピークがテイラーの基準に従えば分解能がある(右図参照)。したがって、ファブリ・ペロー共振器のローレンツィアンフィネスは次のように定義される[ 7]
F
c
=
Δ
ν
FSR
Δ
ν
c
=
2
π
−
ln
(
R
1
R
2
)
.
{\displaystyle {\mathcal {F}}_{c}={\frac {\Delta \nu _{\text{FSR}}}{\Delta \nu _{c}}}={\frac {2\pi }{-\ln(R_{1}R_{2})}}.}
これは上図の青線にあたる。ローレンツィアンフィネス ℱc は、エアリー分布を構成するローレンツィアンピークがどれほどの分解能を持つかという物理的に重要な意味を持つ。式
Δ
ν
c
=
Δ
ν
F
S
R
⇒
R
1
R
2
=
e
−
2
π
≈
0.001867
{\displaystyle \Delta \nu _{c}=\Delta \nu _{FSR}\Rightarrow R_{1}R_{2}=e^{-2\pi }\approx 0.001867}
が成り立つ点において ℱc = 1 が成り立ち、単純エアリー分布のスペクトル分解能に関するテイラーの基準が限界に達する。二つの鏡の反射率が同一であれば、この点は R 1 = R 2 ≈ 4.32%
[ 編集 ] エアリーフィネス ℱAiry の物理的意味[ 7] m を整数とするとき、もし一連の周波数 ν m ν q m Δν Airy Δν Airy だけ離れていれば分解能についてのテイラーの基準が成り立つ。分解可能な信号の最大数が ℱAiry である。この図に示す例では ℱAiry = 6 という整数値になるよう反射率を R 1 = R 2 = 0.59928m = ℱAiry ν q Airy Δν Airy =ν q ν FSR の信号は ν q 周波数に依存する反射率(上図)を持つ鏡を用いたファブリ・ペロー共振器の例。下図にはモード指数 q = 2000, 2001, 2002γ ′q , transA ′[ 7] ファブリ・ペロー共振器を掃引干渉計として用いる場合、つまり共振器の長さ(もしくは入射角)を掃引しつつ用いるとき、ある自由スペクトル領域内のいくつかのピークを光学上見わけることができる。複数の周波数に対応するそれぞれのエアリー分布 A ′trans (ν )Δν Airy とエアリーフィネス ℱAiry である。エアリー分布 A ′trans (ν )Δν Airy は以下のように計算される[ 7]
Δ
ν
Airy
=
Δ
ν
FSR
2
π
(
1
−
R
1
R
2
2
R
1
R
2
4
)
{\displaystyle \Delta \nu _{\text{Airy}}=\Delta \nu _{\text{FSR}}{\frac {2}{\pi }}\left({\frac {1-{\sqrt {R_{1}R_{2}}}}{2{\sqrt[{4}]{R_{1}R_{2}}}}}\right)}
エアリー線幅 Δν Airy は、線幅とフィネスに関する上図においては緑線で表わされている。
Δν Airy = Δν FSR のとき(エアリー分布 A ′trans R 1 R 2
Δ
ν
A
i
r
y
=
Δ
ν
F
S
R
⇒
1
−
R
1
R
2
2
R
1
R
2
4
=
1
⇒
R
1
R
2
≈
0.02944
{\displaystyle \Delta \nu _{Airy}=\Delta \nu _{FSR}\Rightarrow {\frac {1-{\sqrt {R_{1}R_{2}}}}{2{\sqrt[{4}]{R_{1}R_{2}}}}}=1\Rightarrow R_{1}R_{2}\approx 0.02944}
二つの鏡の反射率が等しい場合、これは R 1 = R 2 ≈ 17.2%A ′trans
ファブリ・ペロー共振器のエアリー分布のフィネスは線幅とフィネスに関する上図においては右のグラフに緑線で、青線のローレンツィアンフィネス ℱc と共に表わされている。これは次のように定義される[ 7]
F
A
i
r
y
=
Δ
ν
F
S
R
Δ
ν
A
i
r
y
=
π
2
[
arcsin
(
1
−
R
1
R
2
2
R
1
R
2
4
)
]
−
1
{\displaystyle {\mathcal {F}}_{Airy}={\frac {\Delta \nu _{FSR}}{\Delta \nu _{Airy}}}={\frac {\pi }{2}}\left[\arcsin \left({\frac {1-{\sqrt {R_{1}R_{2}}}}{2{\sqrt[{4}]{R_{1}R_{2}}}}}\right)\right]^{-1}}
ファブリ・ペロー共振器の長さ(もしくは入射角)を掃引する際、エアリーフィネスは自由スペクトル領域内に個々の周波数 ν m
Δ
ν
A
i
r
y
=
Δ
ν
F
S
R
{\displaystyle \Delta \nu _{Airy}=\Delta \nu _{FSR}}
F
A
i
r
y
=
1
{\displaystyle {\mathcal {F}}_{Airy}=1}
A ′trans Δν Airy を導く際、sin(φ ) ≈ φ とする不必要な近似がよく用いられる。先述の厳密解とは異なり、この近似式は以下のようになる。
Δ
ν
A
i
r
y
≈
Δ
ν
F
S
R
1
π
1
−
R
1
R
2
R
1
R
2
4
⇒
F
A
i
r
y
=
Δ
ν
F
S
R
Δ
ν
A
i
r
y
≈
π
R
1
R
2
4
1
−
R
1
R
2
.
{\displaystyle \Delta \nu _{Airy}\approx \Delta \nu _{FSR}{\frac {1}{\pi }}{\frac {1-{\sqrt {R_{1}R_{2}}}}{\sqrt[{4}]{R_{1}R_{2}}}}\Rightarrow {\mathcal {F}}_{Airy}={\frac {\Delta \nu _{FSR}}{\Delta \nu _{Airy}}}\approx \pi {\frac {\sqrt[{4}]{R_{1}R_{2}}}{1-{\sqrt {R_{1}R_{2}}}}}.}
上図では赤線で表わしたこの近似式は、低反射率領域において正しい曲線と解離し、
Δ
ν
A
i
r
y
>
Δ
ν
F
S
R
{\displaystyle \Delta \nu _{Airy}>\Delta \nu _{FSR}}
より一般のファブリ・ペロー共振器の場合、鏡の反射率が全ての周波数で同じとは見做せないこともあるが、ここまでの方程式は減衰時定数 τ c (ν )Δν c (ν ) が周波数の局所関数となる以外は成り立つ。この場合においてもエアリー分布は全てのモードプロファイルの総和となるが、各モードプロファイルは強く歪曲される[ 7] A ′trans γ ′q , trans
γ
q
,
t
r
a
n
s
′
(
ν
)
{\displaystyle \gamma _{q,trans}^{\prime }(\nu )}
[ 編集 ] ファブリ・ペローのエタロン。エタロンに入射する光は多重内部反射を受け、反射および透過する。 エタロンの透過率の波長依存性は、2つの反射面の間で多重に反射された光同士の干渉 により引き起こされる。これらの光の位相が合えば、透過光に強め合う干渉が起こりエタロンの高透過率ピークが生じる。透過光の位相 が逆位相となれば、弱め合う干渉が起こり透過率の谷が生じる。多重反射光の位相が合うかどうかは光の(真空中での)波長 (λ ) エタロンを通過する光の角度 (θ ) エタロンの厚さ (ℓ ) そして反射面の間の材質の屈折率 (n ) によって決まる。
隣りあう透過光(たとえば図のT2 - T1)の間の位相差 δ は下式で与えられる[ 10]
δ
=
(
2
π
λ
)
2
n
ℓ
cos
θ
{\displaystyle \delta =\left({\frac {2\pi }{\lambda }}\right)2n\ell \cos \theta }
両方の反射面が同じ反射率 R をもつとすると、エタロンの透過係数 (英語版 )
T
e
=
(
1
−
R
)
2
1
−
2
R
cos
δ
+
R
2
=
1
1
+
F
sin
2
(
δ
2
)
{\displaystyle T_{\mathrm {e} }={\frac {(1-R)^{2}}{1-2R\cos \delta +R^{2}}}={\frac {1}{1+F\sin ^{2}\left({\frac {\delta }{2}}\right)}}}
ここで、
F
=
4
R
(
1
−
R
)
2
{\displaystyle F={\frac {4R}{(1-R)^{2}}}}
は「フィネス係数」である。
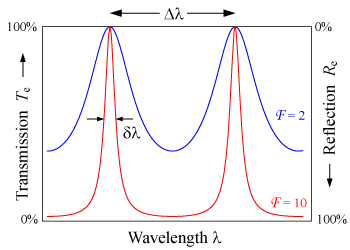
エタロンの透過係数の波長依存性。高フィネスエタロン(赤線)は低フィネスエタロン(青線)に比べて鋭いピークを示し、最低値も小さい。 透過率が最大 (T e = 1光路長 差 (2nl cosθ R e T e + R e = 1
R
max
=
1
−
1
1
+
F
=
4
R
(
1
+
R
)
2
{\displaystyle R_{\max }=1-{\frac {1}{1+F}}={\frac {4R}{(1+R)^{2}}}}
また、反射率が最大となるのは光路長差が波長の半整数 倍になったときである。
隣合う透過率ピーク間の波長差 Δλ は自由スペクトル領域 (英語版 ) 英 : Free Spectral Range, FSR )と呼ばれ、以下のように与えられる。
Δ
λ
=
λ
0
2
2
n
g
ℓ
cos
θ
+
λ
0
≈
λ
0
2
2
n
g
ℓ
cos
θ
{\displaystyle \Delta \lambda ={\frac {\lambda _{0}^{2}}{2n_{\mathrm {g} }\ell \cos \theta +\lambda _{0}}}\approx {\frac {\lambda _{0}^{2}}{2n_{\mathrm {g} }\ell \cos \theta }}}
ここで、 λ 0 n g 群屈折率 である[要出典 。FSRと半値全幅 δλ との関係はフィネスによって以下のように与えられる。
F
=
Δ
λ
δ
λ
=
π
2
arcsin
(
1
F
)
{\displaystyle {\mathcal {F}}={\frac {\Delta \lambda }{\delta \lambda }}={\frac {\pi }{2\arcsin \left({\frac {1}{\sqrt {F}}}\right)}}}
この式は R > 0.5近似 することが多い。
F
≈
π
F
2
=
π
R
1
2
1
−
R
{\displaystyle {\mathcal {F}}\approx {\frac {\pi {\sqrt {F}}}{2}}={\frac {\pi R^{\frac {1}{2}}}{1-R}}}
2つの反射面が同一でなかった場合、フィネスは以下のようになる。
F
≈
π
(
R
1
R
2
)
1
4
1
−
(
R
1
R
2
)
1
2
{\displaystyle {\mathcal {F}}\approx {\frac {\pi (R_{1}R_{2})^{\frac {1}{4}}}{1-(R_{1}R_{2})^{\frac {1}{2}}}}}
フィネスが高いエタロンは透過率ピークが鋭く透過率の最低値も低い。入射角が斜めの場合、R はフレネルの式 で与えられ、一般にはs偏光 とp偏光 で異ることからフィネスも入射光の偏光に依存する。
ファブリ・ペロー干渉計とファブリ・ペローのエタロンとの違いは反射面間の距離 ℓ を調整することで透過ピーク周波数を変化させることができることである。透過率は角度依存するため、エタロンをビームに対して回転させることによっても周波数を変えることができる。
ファブリ・ペロー干渉計またはエタロンは光モデム 、分光器 、レーザー 、天文学 において応用されている。
似た機器にジル・トルノアのエタロン がある。
シリコン (n = 3.4 空気中の高屈折率誘電体スラブの偽色過渡解析。厚さおよび周波数は赤(上)および青(下)では透過光が最大に、緑(中)では最小になるように選んである。 右図に2つの透過光線、T 0 光線 、T 1 √ R √ R エネルギー保存則 から T + R = 1 が要請される。以下では、 n はエタロン内部の屈折率、 n 0 n > n 0 振幅 をフェーザ表示 を用いて表わすものとする。すると、点 b における透過光の振幅は以下のようになる。
t
0
=
T
e
i
k
ℓ
/
cos
θ
{\displaystyle t_{0}=T\,e^{ik\ell /\cos \theta }}
ここで、エタロン内部における波数
k
=
2
π
n
/
λ
{\displaystyle k=2\pi n/\lambda }
λ は真空 中での光の波長である。同様に、点cでの透過光の振幅は以下のようになる。
t
1
′
=
T
R
e
3
i
k
ℓ
/
cos
θ
{\displaystyle t'_{1}=TR\,e^{3ik\ell /\cos \theta }}
2つの光線の方向に垂直 な線上における振幅を足し合わせれば、透過光の全体の振幅が得られる。よって、点bにおける振幅 t 0 t ′1
k
0
ℓ
0
{\displaystyle k_{0}\ell _{0}}
k
0
=
2
π
n
0
/
λ
{\displaystyle k_{0}=2\pi n_{0}/\lambda }
t 0
t
1
=
T
R
e
3
i
k
ℓ
/
cos
θ
−
i
k
0
ℓ
0
{\displaystyle t_{1}=TR\,e^{3ik\ell /\cos \theta -ik_{0}\ell _{0}}}
ここで ℓ 0
ℓ
0
=
2
ℓ
tan
θ
sin
θ
0
{\displaystyle \ell _{0}=2\ell \tan \theta \sin \theta _{0}\,}
この2つの光線の間の位相差は
δ
=
2
k
ℓ
cos
θ
−
k
0
ℓ
0
{\displaystyle \delta ={2k\ell \over \cos \theta }-k_{0}\ell _{0}\,}
θ θ 0 スネルの法則 により
n
sin
θ
=
n
0
sin
θ
0
{\displaystyle n\sin \theta =n_{0}\sin \theta _{0}\,}
よって、位相差は次のように書ける。
δ
=
2
k
ℓ
cos
θ
{\displaystyle \delta =2k\ell \,\cos \theta \,}
ここまでにみてきた係数をくりかえし掛け合わせれば、m 次の透過光線の振幅は以下のように得られる。
t
m
=
T
R
m
e
i
m
δ
{\displaystyle t_{m}=TR^{m}e^{im\delta }\,}
よって、透過光全体の振幅はこれらを全て足し上げて得られ、以下のようになる。
t
=
∑
m
=
0
∞
t
m
=
T
∑
m
=
0
∞
R
m
e
i
m
δ
{\displaystyle t=\sum _{m=0}^{\infty }t_{m}=T\sum _{m=0}^{\infty }R^{m}\,e^{im\delta }}
幾何級数 を解くと、さらに次のように書き下される。
t
=
T
1
−
R
e
i
δ
{\displaystyle t={\frac {T}{1-Re^{i\delta }}}}
透過光の強度は t とその複素共役 を掛け合せれば得られる。入射光の振幅を1としたので、透過係数は以下のように得られる。
T
e
=
t
t
∗
=
T
2
1
+
R
2
−
2
R
cos
δ
{\displaystyle T_{e}=tt^{*}={\frac {T^{2}}{1+R^{2}-2R\cos \delta }}}
キャビティが非対称の場合、つまり2つの反射面の反射率が異なる場合は次のように一般化される。
T
e
=
T
1
T
2
1
+
R
1
R
2
−
2
R
1
R
2
cos
δ
{\displaystyle T_{e}={\frac {T_{1}T_{2}}{1+R_{1}R_{2}-2{\sqrt {R_{1}R_{2}}}\cos \delta }}}
γ
=
ln
(
1
R
)
{\displaystyle \gamma =\ln \left({\frac {1}{R}}\right)}
T
e
=
T
2
1
−
R
2
(
sinh
γ
cosh
γ
−
cos
δ
)
{\displaystyle T_{e}={\frac {T^{2}}{1-R^{2}}}\left({\frac {\sinh \gamma }{\cosh \gamma -\cos \delta }}\right)}
第二項は巻き込みローレンツ分布 (英語版 ) ローレンツ関数 により展開できる。
T
e
=
2
π
T
2
1
−
R
2
∑
ℓ
=
−
∞
∞
L
(
δ
−
2
π
ℓ
;
γ
)
{\displaystyle T_{e}={\frac {2\pi \,T^{2}}{1-R^{2}}}\,\sum _{\ell =-\infty }^{\infty }L(\delta -2\pi \ell ;\gamma )}
ここで、ローレンツ関数は以下のように定義される。
L
(
x
;
γ
)
=
γ
π
(
x
2
+
γ
2
)
{\displaystyle L(x;\gamma )={\frac {\gamma }{\pi (x^{2}+\gamma ^{2})}}}
^ ペローの名前は科学論文などではアクセント付きで Pérot のように綴られることが多く、この干渉計を英語表記する場合も同様にアクセント付きで表記されることが多い。
^ Métivier, Françoise (September–October 2006). “Jean-Baptiste Alfred Perot” (フランス語) (pdf). Photoniques (25). オリジナル の2007年11月10日時点におけるアーカイブ。. https://web.archive.org/web/20071110003132/http://www.sabix.org/documents/perot.pdf 2007年10月2日 閲覧。 ^ Fabry, C; Perot, A (1899). “Theorie et applications d'une nouvelle methode de spectroscopie interferentielle”. Ann. Chim. Phys 16 (7). ^ Perot, A; Fabry, C (1899). “On the Application of Interference Phenomena to the Solution of Various Problems of Spectroscopy and Metrology” . Astrophysical Journal 9 . http://adsabs.harvard.edu/full/1899ApJ.....9...87P . ^ オックスフォード英語辞典 ^ Williams, Benjamin S. (2007). “Terahertz quantum-cascade lasers”. Nature Photonics 1 (9): 517–525. doi :10.1038/nphoton.2007.166 . ISSN 1749-4885 . ^ a b c d e f g h i j k l m n o p q r s t u v w Ismail, Nur; Kores, Cristine Calil; Geskus, Dimitri; Pollnau, Markus (7 2016). “Fabry-Pérot resonator: spectral line shapes, generic and related Airy distributions, linewidths, finesses, and performance at low or frequency-dependent reflectivity” . Opt. Express 24 (15): 16366–16389. doi :10.1364/OE.24.016366 . http://www.opticsexpress.org/abstract.cfm?URI=oe-24-15-16366 .
^ a b Siegman, A. E. (1986). “ch. 11.3”. Lasers . Mill Valley, California: University Science Books. pp. 413–428
^ Svelto, O. (2010). “ch. 4.5.1”. Principles of Lasers (5th ed.). New York: Springer. pp. 142–146 ^ Lipson, S.G.; Lipson, H.; Tannhauser, D.S. (1995).
Hernandez, G. (1986). Fabry–Pérot Interferometers . Cambridge: Cambridge University Press. ISBN 0-521-32238-3 . 



















































![{\displaystyle \Delta \nu _{\text{Airy}}=\Delta \nu _{\text{FSR}}{\frac {2}{\pi }}\left({\frac {1-{\sqrt {R_{1}R_{2}}}}{2{\sqrt[{4}]{R_{1}R_{2}}}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29a3f93285275d6dbdb0d74e7880666ef837d119)
![{\displaystyle \Delta \nu _{Airy}=\Delta \nu _{FSR}\Rightarrow {\frac {1-{\sqrt {R_{1}R_{2}}}}{2{\sqrt[{4}]{R_{1}R_{2}}}}}=1\Rightarrow R_{1}R_{2}\approx 0.02944}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d75581aa58b0caf1f47f94e8413da3ac9f98a5da)
![{\displaystyle {\mathcal {F}}_{Airy}={\frac {\Delta \nu _{FSR}}{\Delta \nu _{Airy}}}={\frac {\pi }{2}}\left[\arcsin \left({\frac {1-{\sqrt {R_{1}R_{2}}}}{2{\sqrt[{4}]{R_{1}R_{2}}}}}\right)\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c79f104e67cc2ecba7fd92a6fe0136a949216ad8)


![{\displaystyle \Delta \nu _{Airy}\approx \Delta \nu _{FSR}{\frac {1}{\pi }}{\frac {1-{\sqrt {R_{1}R_{2}}}}{\sqrt[{4}]{R_{1}R_{2}}}}\Rightarrow {\mathcal {F}}_{Airy}={\frac {\Delta \nu _{FSR}}{\Delta \nu _{Airy}}}\approx \pi {\frac {\sqrt[{4}]{R_{1}R_{2}}}{1-{\sqrt {R_{1}R_{2}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2b0eb4601531b5be0be103546064c11c3d6fca4)




























