ヒルベルトの無限ホテルのパラドックス

ヒルベルトの無限ホテルのパラドックス(ヒルベルトのむげんホテルのパラドックス、英: Hilbert's Infinite Hotel Paradox)とは、無限集合の非直観的な性質を説明する思考実験である。無限個の客室があるホテルは「満室」でも(無限人の)新たな客を泊めることができ、その手順を無限に繰り返せることを示す。論理的・数学的に正しいが、直観に反するという意味でのパラドックス(擬似パラドックス)である。ヒルベルトのグランドホテルのパラドックス(英: Hilbert's paradox of the Grand Hotel)、ヒルベルトホテル(英: Hilbert's Hotel)とも。1924年にダフィット・ヒルベルトが論文「Über das Unendliche(無限について)」で導入し[1]、1947年のジョージ・ガモフの著書「1、2、3…無限大」によって広まった[2][3]。
簡単のため、以下の記述では無限とは可算無限を意味するものとする。しかし選択公理を仮定すれば、任意の無限集合は可算無限集合を部分集合にもつため、非可算無限の場合でも少し議論を修正するだけでよい。
パラドックスの内容
[編集]無限個の客室があり、「満室」である仮想的なホテルを考える。客室数が有限の場合、「満室であること」と「新たに来た客を泊められないこと」は同値だが(鳩の巣原理)、無限ホテルではそうはならない。
有限人の新たな客
[編集]1人の客が来てホテルに宿泊を希望したとする。そこで1号室の客を2号室に、2号室の客を3号室に、n号室の客を(n + 1)号室に(同時に)移動させる。すると1号室は空室になり、1人の客を泊めることができる。この手順を繰り返すことで、任意の有限人の新たな客の部屋を作れる。
無限人の新たな客
[編集]
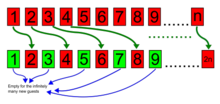
また、無限人の新たな客を泊めることも可能である。1号室の客を2号室に、2号室の客を4号室に、n号室の客を2n号室に移動させれば、すべての奇数号室(可算無限個ある)が新たな客に解放される。
それぞれ無限人の客を乗せた無限台のバス
[編集]いくつかの方法で、それぞれ無限人の乗客を乗せた無限台のバスの団体客を泊めることが可能である。ほとんどの方法はバスの座席が番号付けされていること(可算選択公理)を仮定する。一般にこの問題を解くには任意の対関数が使える。それぞれの方法で、乗客の座席番号をn、乗っているバスの号車番号をcとすると、nとcが対関数の2つの引数になる。
素数冪を用いる方法
[編集]i号室の客を2i号室に移動させて奇数号室を空け、1号車の団体客を3n号室に、2号車の団体客を5n号室に、一般にc号車の団体客を、c番目の奇素数をpとして、pn号室に泊める。この方法ではいくつかの客室が空室になる(それがホテルにとって有益かはともかく)。具体的には15や847などのすべての素数冪でない奇数号室は誰も泊まっていない状態になる(よって厳密な議論では、これは来客者数が最初に空けた客室数に等しいかそれより少ないことを示している。正確に合うようにアルゴリズムを修正するよりも、これとは独立に、来客者数が最初に空けた客室数に等しいかそれより多いことを示し、したがってそれらが等しいことを示す方が簡単である)(このアルゴリズムはnとcを入れ替えても成り立つが、どちらかを選んで固定し、一貫して適用しなければならない)。
素因数分解を用いる方法
[編集]座席s、号車cの乗客を2s3c号室に泊める(元のホテルの客はc = 0、1号車はc = 1、…とする)。すべての正の整数は一意的に素因数分解できるので(算術の基本定理)、すべての客が部屋に入り、同じ部屋に2人入らないことがわかる。たとえば2592 (2534) 号室の客は、4号車の5番目の席に座っていた乗客である。素数冪を用いる方法と同様に、この方法ではいくつかの客室が空室になる。
この方法は無限の夜に、無限の入り口に…などの問題に簡単に拡張できる (2s3c5n7e)。
Interleaving method
[編集]それぞれの乗客について、十進法などの任意の位取り記数法で表したnとcの桁数を比較し(元のホテルの客はc = 0とする)、桁数が異なる場合、同じ桁数になるまで桁数の少ない方の先頭に0を付け加える。そして[号車番号の1桁目]-[座席番号の1桁目]-[号車番号の2桁目]-[座席番号の2桁目]-…と各桁の数字をinterleaveして部屋番号を生成する。元のホテルの(0号車の)1729号室の客は、01070209号室(すなわち1,070,209号室)に移動する。789号車の1234番目の座席の乗客は01728394号室(すなわち1,728,394号室)に入る。
素数冪を用いる方法とは異なり、この方法は客室を完全に埋め、interleaving processを逆にすることで、元の号車と座席を復元することができる。まず部屋番号が奇数桁の場合、先頭に0を追加する。すると号車番号は奇数桁目の数字からなり、座席番号は偶数桁目の数字からなる。もちろん元の符号化の方法は任意であり、一貫して適用する限り、2つの数字の役割を逆にすることができる(座席を奇数桁目にして号車を偶数桁目にする)。
三角数を用いる方法
[編集]元のホテルの客を(n2 + n)/2(すなわちn番目の三角数)号室に移動する。バスの団体客を[(c + n - 1)2 + (c + n - 1)]/2 + n(すなわち(c + n - 1)番目の三角数 + n)号室に泊める。これですべての客室が重複なく埋まる。
この対関数は、ホテルを1部屋分の奥行きがある無限に高いピラミッドとして構造化することでイメージできる。ピラミッドの最上段に1号室があり、次の段に2号室と3号室があり、以下同様に続く。右端の客室の集合からなる列が三角数号室に対応する。それらの客室が(元のホテルの客が移動して)埋まると、空になった部屋は元の形と厳密に等しいピラミッドの形になる。よって、この手順を各無限集合(バス)ごとに繰り返すことができる。これを1台ずつ行うには無限のステップ数が必要になるが、事前の計算式を用いることで、手順の中で自分のバスの順番が来た時点で乗客は自分の部屋が何番に「なる」か決定でき、ただちにそこに行くことができるようになる。
任意の列挙方法
[編集]とする。は可算なのでSは可算であり、その要素s1, s2, ...を列挙することができる。ここでsn = (a, b)とし、a号車のb番目の乗客をn号室に割り当てる(元のホテルの客はa = 0とする)。これで全員を客室に割り当てる関数ができ、なおかつ、この割り当てはどの客室ももらさない。
さらなる無限の階層
[編集]ホテルが海に隣接していて、無限隻のカーフェリーが来て、それぞれ無限台のバスが積み込まれており、それぞれ無限人の乗客が乗っているとする。これは3「段階」の無限を含む状況であり、これまでの方法の拡張で解くことができる。
素因数分解を用いる方法は、無限の階層が増えるごとに新たな素数を追加することで適用できる(2s3c5f、フェリーの番号をfとする)。
素数冪を用いる方法は、さらなる素数の冪乗をとることで適用でき、結果として小さな入力でも非常に大きな部屋番号になる。たとえば、2番目の座席-3番目のバス-2番目のフェリー(番地2-3-2)に該当する乗客の部屋番号は、572 = 549(底は2番目の奇素数である5、指数は3番目の奇素数である7の2乗 = 49)となり、17,763,568,394,002,504,646,778,106,689,453,125号室に行くことになる。
interleaving methodでは、2つではなく3つのinterleaveされた「strands」を用いる。番地2-3-2の乗客は232号室に行き、番地4935-198-82217の乗客は008,402,912,391,587号室(先頭のゼロは除ける)に行くことになる。
任意の階層数の無限人の客が来る可能性を想定して、ホテルは何人の客が後に来ても移動する必要がないような部屋を割り当てたいと思うかもしれない。一つの解決策は、各来客者の番地を二進数に変換し、1を各階層の開始地点のセパレータとして使用し、0を並べて階層内の番号(たとえば客の号車番号)を表現することである。たとえば番地2-5-1-3-1(5つの無限の階層)の客は、10010000010100010(十進数で295458)号室に行くことになる。
この手順の追加ステップとして、番号の各節から0を1つ削除することができる。この例では客の部屋は101000011001(十進数で2585)号室となる。これによりすべての部屋が想定される客によって埋まることが保証される。もし無限人の客の集合が来ない場合は、2の冪の番号の部屋のみが使用される。
無限に入れ子になった階層
[編集]無限人の客が有限回入れ子になっている場合は部屋を作れるが、各階層の客が有限人だったとしても無限回入れ子になっている場合は常にそうとは限らない(客が3.271260067…のように無理数でコーディングされる場合その集合は非可算になり得る)。
考察
[編集]ヒルベルトのパラドックスは擬似パラドックスである。直観に反するが真であると証明される結論を導く。文「すべての部屋に客がいる」と「これ以上客を泊められない」は、部屋が無限にある場合は同値ではない。
最初はこの状態は非直観的に思えるかもしれないが、「無限のものの集まり」と「有限のものの集まり」の性質はまったく異なる。ヒルベルトの無限ホテルのパラドックスは、カントールの超限数の理論を用いて理解することができる。複数の部屋がある現実の(有限の)ホテルでは、奇数番号の部屋数は部屋の総数より明らかに少ないが、ヒルベルトいうところの無限ホテルでは、奇数番号の部屋数は部屋の総「数」より少なくない。数学用語でいうと、奇数番号の部屋全体を含む部分集合の濃度は、すべての部屋の集合の濃度と等しい。実際、無限集合は等しい濃度の真部分集合をもつ集合として特徴づけられる。可算集合(自然数全体と等しい濃度の集合)の場合、その濃度は(アレフ・ゼロ)である[4]。
言い換えれば、任意の可算無限集合Sについて、Sが自然数全体を真部分集合として含んでいたとしても、Sを自然数全体の集合に写像する全単射が存在するということである。たとえば、有理数(整数の分数で表せる数)全体の集合は、真部分集合として自然数全体を含むが、有理数全体は可算なので自然数全体の集合より大きくない(自然数全体から有理数全体への全単射が存在する)。
フィクションでの言及
[編集]- BBC Learning Zoneでは、1996年の単発の教育ドキュメンタリードラマ「Hotel Hilbert」を繰り返し放送した。若い女性客フィオナ・ナイト(英: Fiona Knight、finite(有限)のもじり)の目を通して見たホテルを舞台にしている。この番組は視聴者に無限の概念について教育することを目的としたものだった。
- 数学者・SF作家ルーディ・ラッカーの小説『ホワイト・ライト』には、ヒルベルトのパラドックスを元にしたホテルが登場し、物語の主人公がゲオルク・カントールに出会う場面がある。
- スティーヴン・バクスターのSF小説『トランセンデント』には、ホテルではなく宇宙船の戦士を用いるように修正されたパラドックスに基づく説明で、無限の性質についての簡単な議論がある。
- ジェフリー・A・ランディスのネビュラ賞受賞短編小説「ディラック海のさざなみ」では、無限に満たされたディラックの海がなお粒子を受け入れることができる理由の説明としてヒルベルトホテルを使用している。
- ペーター・ホゥの小説「スミラの雪の感覚」では、表題のヒロインはホテルの支配人と客が、遅れてきた者が自分の部屋とプライバシーを確保できるようにわざわざ手間をかけるのは立派なことだと思案している。
- イーヴァル・エクランドの児童向け小説『The Cat in Numberland』では、「ミスター・ヒルベルト」と彼の妻がすべての整数のために無限ホテルを経営している。物語は有理数に対する三角数を用いる方法を使って進んでいく。
- ウィル・ワイルズの小説『時間のないホテル』では無限に大きいモーテルを題材にしてるが、悪役の名前は「ヒルベルト」である。
- レジナルド・ヒルの小説『異人館』では登場人物・サムがヒルベルトホテルのパラドックスに言及している。
- ナウム・ヤコブレヴィチ・ヴィレンキンの短編小説『不思議なホテル』(しばしばスタニスワフ・レムの作品と誤認される)では、ヒルベルトの無限ホテルが無限人の新たな主人が来たときに再編される方法を示している。
- ジョン・ロデリックとケン・ジェニングスはオムニバス・ポッドキャストの中の配信「The Hilbert Hotel Entry」でこのホテルについて議論した。
- アラン・ムーアとケヴィン・オニールの漫画『リーグ・オブ・エクストラオーディナリー・ジェントルメン』シリーズの第四篇「テンペスト」には、インフィニティと呼ばれる悪役が登場する。物語では悪役がヒルベルトのパラドックスを元にしたホテルに行くことが示唆されている。ゲオルク・カントールについても言及されている。
- 倉多江美のマンガ『一万十秒物語』には無限ホテルをテーマにした短篇がある。
脚注
[編集]- ^ Hilbert 2013, p. 730で復刻。
- ^ Kragh 2014.
- ^ Gamow 1947, p. 17.
- ^ Rucker 1984, pp. 73–78.
参考文献
[編集]- Gamow, George (1947). One Two Three... Infinity: Facts and Speculations of Science. ニューヨーク: ヴァイキング・プレス
- Hilbert, David (2013). Ewald, William; Sieg, Wilfried. eds. David Hilbert’s Lectures on the Foundations of Arithmetics and Logic 1917-1933. ハイデルベルク: シュプリンガー・フェアラーク. doi:10.1007/978-3-540-69444-1. ISBN 978-3-540-20578-4
- Kragh, Helge (2014). "The True (?) Story of Hilbert's Infinite Hotel" (英語). arXiv:1403.0059。
- Rucker, Rudy (1984) [1982]. Infinity and the Mind. The Science and Philosophy of the Infinite. パラディン・プレス. ISBN 0-586-08465-7
関連項目
[編集]外部リンク
[編集]- 数学の中の無限 — 無限の中の数学 - 集合論研究者・渕野昌による文書。ヒルベルトホテルについて触れられている。
- “ 無限ホテル ”のパラドックス - ジェフ・デコフスキーによるTED-Edレッスン。



