ベクトル束
数学において、ベクトル束(べくとるそく、英: vector bundle; ベクトルバンドル)は、ある空間 X(例えば、X は位相空間、多様体、代数多様体等)により径数付けられたベクトル空間の族を作るという方法で与えられる幾何学的構成である。
導入
[編集]空間 X 上のベクトル束(ベクトルバンドル)とは、X の各点 x にベクトル空間 V(x) を対応させた(というよりは「貼り付けた」("attach"))とき、それらが「うまく貼り合わされて」もとの X と同種の空間(例えば、位相空間、多様体、代数多様体等)を成すようなものである(「バンドル」は一まとめに束ねたものの意)。
最も単純な例は、貼り合せるベクトル空間の族が一定の(つまり固定したベクトル空間 V により、すべての x ∈ X に対し V(x) = V となる)場合である。このとき、各点 x ∈ X に対応する V の複写の全体が貼り合わされて X 上のベクトル束 X × V ができる。この様なベクトル束は自明であると言われる。
より複雑(かつ原型的)な例の一つのクラスは、滑らかな多様体(可微分多様体)の接束である。これは多様体 M の各点 x ∈ M に、その点での接空間 TxM を付随させたものである。接束は一般には自明束ではない。たとえば、二次元球面の接束は毛玉の定理により自明ではない。一般に、多様体の接束が自明となることを「多様体は平行化可能 (parallelizable) である」と言い表す。
ベクトル束は殆ど常に局所的に自明である必要があるが、これはベクトル束が、ベクトル空間をファイバーとするファイバー束(ファイバーバンドル)であることを意味する。また、ベクトル空間として実数体または複素数体上のベクトル空間を考えるのが普通であり、そのようなベクトル束は、それぞれ実ベクトル束または複素ベクトル束と呼ばれる。複素ベクトル束を、付加構造を備えた実ベクトル束として見ることもできる。以下では、位相空間の圏における実ベクトル束に焦点を絞って議論する。
定義および定義からただちに証明されること
[編集]実ベクトル束は、
- 底空間(ていくうかん、base space)と呼ばれる位相空間 X および全空間(ぜんくうかん、total space)と呼ばれる位相空間 E
- 束射影(そくしゃえい、bundle projection)あるいは単に射影と呼ばれる連続写像 π: E → X
- 任意の x ∈ X に対し、ファイバー π−1({x}) に与えられた実ベクトル空間としての構造
の組であって(ただし、紛れのおそれの無い場合には束射影の記号で代表して、ベクトル束 π: E → X あるいは全空間で代表してベクトル束 E のように呼ぶ)、以下の整合性条件:
任意の x ∈ X に対し、開近傍 U, 正整数 k, 同相写像
が存在し、任意の y ∈ U に対して、
- 任意の v ∈ Rk に対して π(φ(y, v)) = y かつ
- 写像 はベクトル空間の同型写像である。
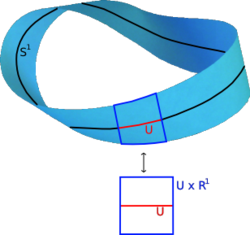
を満たすものである。開近傍 U に同相写像 φ を考え合わせたものを、ベクトル束の局所自明化 (local trivialisation) という。局所自明化によって、写像 π が「局所的に見れば」 U × Rk から U の射影である「かのようにみえる」ということが表されている。
任意の x ∈ X に対し、ファイバー π−1(x) は有限次元の実ベクトル空間であり、従って実ベクトル空間としての次元 kx を有する。局所自明性により、関数 は局所定数であり、従って X の各連結成分の上では一定である。任意の x ∈ X に対し、kx が定数 k に等しいとき、k をベクトル束 E の階数(かいすう、rank)といい、E は階数 k のベクトル束であるという。階数 1 のベクトル束は、直線束 (line bundle) と呼ばれる。階数 2 のベクトル束は稀に平面束 (plane bundle) とも呼ばれる。
直積 X × Rk に自然な射影 X × Rk → X を考えたものはベクトル束であり、X 上の階数 k の自明束(じめいそく、trivial bundle)という。
座標変換式
[編集]階数 k のベクトル束 E → X と、近傍の対 U, V にそれぞれの局所自明化
が与えられているとき、U ∩ V 上で合成写像
は矛盾無く定まり、
を満たす GL(k)-値写像
がとれる。このような写像を(U, V のとり方に依らず総称して)ベクトル束の遷移写像もしくは推移写像 (transition function) または座標変換 (coordinate transformation) という。
座標変換の全体は任意の U, V, W についてその局所自明化上で
を満たすという意味で チェック・コサイクル を成す。したがって、組 (E, X, π, Rk) はファイバー束を定める。このとき、座標変換 gUV の与える付加情報は、ファイバーの構造群が GL(k) であり、ファイバーへの作用が GL(k) の通常の作用として与えられることを示すものである。
逆に、ファイバー束 (E, X, π, Rk) がファイバー Rk 上に GL(k) の通常の作用によるコサイクル作用 (cocycle action) を持つならば、対応するベクトル束が存在する。このことを以ってベクトル束の定義とすることもある。
ベクトル束の射
[編集]ベクトル束 π1: E1 → X1 からベクトル束 π2: E2 → X2 への射 (morphism) は、連続写像 f: E1 → E2 と g: X1 → X2 の対であって、以下の条件を満たすものである。
π1 の全射性により、g は f によって完全に決定される。このことから f は g の被覆と呼ばれる。
ベクトル束全体の成す類に束射を考え合わせたものは圏をなす。ベクトル束を空間が可微分多様体で束射影が滑らかなものに制限し、束の射も滑らかなもののみに制限すると、滑らかなベクトル束の圏を得る。ベクトル束の射は、ファイバー束間の束写像の概念の特別な事例であり、(ベクトル)束準同型(写像) (vector bundle homomorphism) ともいう。
E1 から E2 への束準同型で、その逆写像が再び(E2 から E1 への)束準同型であるものを(ベクトル)束同型(写像) (vector bundle isomonprphism) といい、このとき E1 と E2 とは束(として)同型であるという。 X 上の(階数 k の)ベクトル束と(X 上の階数 k の)自明束の間の同型写像を E の自明化 (trivialisation) といい、自明化をもつベクトル束 E は自明である、または自明化可能 (trivialisable) であるという。ベクトル束の定義より、任意のベクトル束は局所的に自明である。
固定した底空間 X の上のすべてのベクトル束の圏を考えることもできる。 この圏の射として、底空間 X 上の写像が恒等写像になるベクトル束の射を取る。 つまり、以下の図式を可換にする束の射である。
(この圏はアーベル圏ではない。ベクトル束の射の核をベクトル束とする自然な方法は一般に存在しない)
ベクトル束 π1: E1 → X1 からベクトル束 π2: E2 → X2 へのベクトル束の射が、写像 g: X1 → X2 を被覆するとき、この射は、X1 上で E1 から引き戻し束 g∗E2 へのベクトル束の射と見ることもできる。
切断および局所自由層
[編集]
ベクトル束 π: E → X と X の開集合 U が与えられたとき、π の U 上の切断、断面 (section) を考えることができる。切断とは、π ∘ s = idU を満たす連続写像 s: U → E のことであり、これは本質的には U の各点で、それに付随するベクトル空間のベクトルを連続的に対応させることを意味する。例えば、可微分多様体の接束の切断とは、その多様体上のベクトル場に他ならない。
F(U) を、U 上の切断全体の集合とする。F(U) は常に、少なくとも零切断 (zero section)と呼ばれる一つの要素を含む。これは、任意の要素 x ∈ U をベクトル空間 π−1({x}) の零ベクトルに写像する切断 s である。 各点における切断の加法とスカラー倍により、F(U) はそれ自体が実ベクトル空間になる。 これらベクトル空間の(開集合 U に関する)系は、X 上のベクトル空間の層をなす。
s が F(U) に属する切断で α: U → R が連続写像のとき、点ごとのスカラー乗法で定義される αs は再び F(U) に属する。したがって、F(U) を U 上で定義された実数値連続関数環の上の加群と見なすことができる。さらに、X 上の実数値連続関数全体の成す構造層を OX と書くと、F は OX 加群全体の層になる。
どんな OX 加群の層でも、ベクトル束からこの方法で得られるというわけではなく、局所自由であるものに限られる。実際にこの構成法では、局所的には射影 U × Rk → U の切断を求めることになるが、それはちょうど連続写像 U → Rk であって、連続関数 U → R の k 組として表されるからである。
さらに言えば、X 上の実ベクトル束の圏は、局所自由かつ有限生成な OX 加群の層の圏に圏同値である。したがって、X 上の実ベクトル束の圏は OX 加群の層の圏に含まれていると考えることができる。後者はアーベル圏であり、それによってベクトル束の射の核や余核をその中でならば計算することができる。
n-階ベクトル束が自明であるための必要十分条件は、それが n 個の線型独立な大域切断を持つことであることに注意。
ベクトル束の演算
[編集]ベクトル空間に対する演算の多くは、それをファイバーごとに行うことによってベクトル束の演算に拡張することができる。
例えば、E が X 上のベクトル束のとき、x ∈ X におけるファイバー Ex をその双対ベクトル空間 (Ex)∗ に取り替えて、E の双対束 (dual bundle) と呼ばれる X 上のベクトル束 E* が定まる。厳密に言えば、E* は、x ∈ X, φ ∈ (Ex)* に関する対 (x, φ) 全体の成す集合として定義できる。E の局所的自明化の逆像の双対空間は E* の局所的自明化だから、双対束は局所的に自明である。これには双対ベクトル空間を取る操作が関手的であること(ここでは双対をとることと同型写像とが可換ということ)が鍵になっている。
(同じ体上の)二つのベクトル空間の上で行える関手的操作のほとんどは X 上のベクトル束 E, F の対に直接的に拡張することができる。いくつか例を挙げる。
- E と F のホイットニー和 (Whitney sum) または直和束 (direct sum bundle) と呼ばれる X 上のベクトル束 E ⊕ F は、各点 x の上のファイバーがベクトル空間 Ex と Fx の直和 Ex ⊕ Fx となるものとして定義される。
- 同様に、テンソル積束 (tensor product bundle) E ⊗ F が、ファイバーごとにベクトル空間のテンソル積を用いることによって定義できる。
- 準同型束 (Hom-bundle) Hom(E, F) は、x におけるファイバーが Ex から Fx への線型写像全体の空間(Hom(Ex, Fx) または L(Ex, Fx) としばしば書かれる)であるようなベクトル束である。この束をこのように書いて便利に準同型束(あるいは Hom-束)と呼ぶのは、「Hom(E, F) の X 上の切断」と「E から F への X 上のベクトル束の準同型」とが同一視できるためである。
- さらに、自己準同型束 Hom(E, E) の断面 s と関数 f: X → R が与えられると、点 x ∈ X 上のファイバーを線型写像 s(x) : Ex → Ex の f(x)-固有空間とすることで、固有束 (eigenbundle) を構成することができる。
- 双対束 E∗ は E と自明束 R × X との間の準同型束 Hom(E, R × X) に一致する。また、自然なベクトル束の同型 が存在する。
これらの操作は、ベクトル空間の圏における操作の多くが関手的な仕方でベクトル束の圏における操作として意味を成すという、ベクトル束が持つ一般的な特徴を示す特定の例となっている。このことは滑らかな関手の言葉を用いて精緻化することができる。
もっと別な種類の操作として、原像あるいは引き戻し (pull-back bundle) 構成と呼ばれるものがある。ベクトル束 E → Y と連続写像 f: X → Y が与えられたとき、Y 上のベクトル束 E を f によって X 上のベクトル束 f ∗E へ「引き戻す」ことができる。つまり、x ∈ X 上のファイバーは、実質的に f (x) ∈ Y 上のファイバーになっている。これを使えば、ホイットニー和 E ⊕ F を X × X 上のベクトル束として対角線写像 X → X × X の引き戻しとして定義することもできる。
付加構造と一般化
[編集]ベクトル束には、さらにいろいろな構造が与えられていることも多い。例えば、ベクトル束には計量が与えられていることがある。通常は計量が正定値であることを仮定し、これによって E の各ファイバーはユークリッド空間となる。また例えば、複素構造を備えた実ベクトル束は複素ベクトル束に対応する。複素ベクトル束は、実ベクトル束の定義において実ベクトル空間や実線型写像としていたところを代わりに複素ベクトル空間や複素線型写像にとりかえて得られるものである。もっと一般に、ベクトル束に移入された付加構造は、典型的には束の構造群の還元によって得られるものとして理解することができる。(実数体や複素数体だけではなく)さらに一般の位相体上のベクトル束というものも用いられる。
また、有限次元ベクトル空間の代わりにバナッハ空間をファイバー F とすることでバナッハ束の概念がえられる[1]。特に、各ファイバー上の局所自明化に対する条件は(単に線型同型なだけでなく)バナッハ空間の同型とするのが自然であり、さらに座標変換
がバナッハ多様体の間の連続写像となるようにすべきである。同様に、Cp-級ベクトル束の理論では、これらの写像が Cp-級であることを要請する。
ベクトル束は、ファイバーがベクトル空間でコサイクルがベクトル空間構造を保つような特別なファイバー束であった。もっと一般のファイバー束は、そのファイバーとして他のさまざまな構造をとることができる。たとえば、球面によってファイバー付けられるファイバー束は球面束と呼ばれる。
可微分ベクトル束
[編集]ベクトル束 (E, p, M) が滑らか (smooth) であるとは、E と M が滑らかな多様体で p: E → M が滑らかな写像であり、かつ局所自明化が微分同相となるようなときに言う。要求する滑らかさの度合いにより、各種の Cp-級ベクトル束や C∞-級ベクトル束、Cω-級ベクトル束(実解析的ベクトル束)などの異なる概念が得られる。本節では、C∞-級ベクトル束について主に述べる。最も重要な C∞-級ベクトル束の例は、C∞-級多様体 M の接束 (TM, πTM, M) である。
C∞-級ベクトル束 (E, p, M) のもつ非常に重要な性質で、一般の C∞-級ファイバー束が持たないものがある。具体的には、各 v ∈ Ex における接空間 Tv(Ex) は、ファイバー Ex 自身と自然に同一視することができることである。この同一視は
で定義される垂直射あるいは垂直持ち上げ (vertical lift) vlv: Ex → Tv(Ex) によって与えられる。垂直持ち上げは自然に C∞-級ベクトル束の同型 p∗E → VE と見ることができる。ここで (p∗E, p∗p, E) は E 上のベクトル束 (E, p, M) の p: E → M に沿った引き戻し束であり、VE ≔ Ker(p∗) ⊂ TE は垂直接束と呼ばれる、全空間 E の接束 (TE, πTE, E) の自然な部分ベクトル束である。
スリットベクトル束 (slit vector bundle) E/0 はベクトル束 (E, p, M) から零切断 0 ⊂ E を取り除くことで得られ、ここから得られる標準的なベクトル場 Vv ≔ vlvv は標準ベクトル場 (canonical vector field) として知られる。もっときちんと言えば、V はベクトル束 (TE, πTE, E) の滑らかな切断であり、またリー群作用
の無限小生成作用素としても定義される。
任意の滑らかなベクトル束 (E, p, M) に対して、その接束 (TE, πTE, E) の全空間 TE は自然な二次ベクトル束構造 (TE, p∗, TM) を持つ。ここで p∗ は標準射影 p: E → M の押し出し (push-forward) である。この二次ベクトル束構造におけるベクトル束演算は、もとの加法 +: E × E およびスカラー倍 λ: E → E から得られる押し出し +∗: T(E × E) → TE および λ∗: TE → TE である。
K-理論
[編集]位相的 K-理論は位相空間の複素ベクトル束を用いたコホモロジー理論の類似物である。位相空間 X 上の K-理論の群[* 1] K(X) は、X 上の複素ベクトル束 E の同型類 [E] の全体 VecBdlC(X) を生成系とする自由可換群に対して、完全列
- 0 → A → B → C → 0
を持つ全てのベクトル束 A, B, C について与えられる関係式
- [B] = [A] + [C]
を基本関係式として定めて得られる商群である。複素ベクトル束の代わりに実ベクトル束を用いた同様の構成は KO理論という。コンパクト台付き K-理論や、高次の K-理論なども定義することができる。
よく知られるラウル・ボットの周期性定理は任意の位相空間 X の K 理論が X と 2 次元球面 S2 との直積
- X × S2
に同型であることを主張するものである。
代数幾何学において、K 理論の群はスキーム X 上のベクトル束に上記の同値関係をあたえたもののみならず、スキーム上の連接層の全体からも K-理論の群が作られる。台となるスキームが滑らかならばこの二つの構成は同じ群を与える。
関連項目
[編集]一般的事項
[編集]- グラスマン多様体(英語: Grassmannian):ベクトル束の分類空間、特に、直線束に対する射影空間
- 特性類
- 分裂原理(英語: Splitting principle)
位相幾何学、微分幾何学
[編集]- 主束
- ファイバー束:一般的な位相幾何学の概念、特に、被覆空間がある。
- 接続 (ベクトル束):ベクトルバンドルの断面を微分するのに必要な概念
- 層 (数学)
- 位相的K-理論(英語: Topological K-theory)
代数幾何学、解析幾何学
[編集]
脚注
[編集]参考文献
[編集]- ^ Lang, Serge (1995), Differential and Riemannian manifolds, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94338-1
- Hatcher, Allen (2003), Vector Bundles & K-Theory (2.0 ed.)
- Lee, Jeffrey M. (2009), Manifolds and Differential Geometry, Graduate Studies in Mathematics, Vol. 107, Providence: American Mathematical Society . ISBN 978-0-8218-4815-9
- Lee, John M. (2003), Introduction to Smooth Manifolds, New York: Springer, ISBN 0-387-95448-1 see Ch.5
- Jost, Jürgen (2002), Riemannian Geometry and Geometric Analysis (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-42627-1, see section 1.5.
- Abraham, Ralph H.; Marsden, Jerrold E. (1978), Foundations of mechanics, London: Benjamin-Cummings, ISBN 978-0-8053-0102-1, see section 1.5













![{\displaystyle \operatorname {vl} _{v}w[f]:={\frac {d}{dt}}{\Big |}_{t=0}f(v+tw),\quad (f\in C^{\infty }(E_{x}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46804161de2df8e0f97c6aae073b9f0dbaf5022c)
