「ブラッグ曲線」の版間の差分
| 19行目: | 19行目: | ||
ブラッグピークは非常に鋭い。このことは周辺[[組織 (生物学)|組織]]に大きな障害を与えることなく、[[腫瘍]]に対する照射効果が密度の濃いものになりうることを意味する。 |
ブラッグピークは非常に鋭い。このことは周辺[[組織 (生物学)|組織]]に大きな障害を与えることなく、[[腫瘍]]に対する照射効果が密度の濃いものになりうることを意味する。 |
||
図の青い曲線は、例えばエネルギー加速器を調節することによって、照射される腫瘍体積がより大きくなるように、ブラッグピークがどのように広げられるかを示している。 |
図の青い曲線は、例えばエネルギー加速器を調節することによって、照射される腫瘍体積がより大きくなるように、ブラッグピークがどのように広げられるかを示している。 |
||
最後に、 |
最後に、緑の曲線は根本的に赤および青の曲線とは性状が異なっている。すなわち、高エネルギー[[X線]]の吸収動態である。この曲線にはブラッグピークが見られないが、エネルギー強度は裾野の広い[[指数関数]]曲線として捉えることができる。 |
||
<!-- 英語の用語であるストッピングパワー (stopping power) とブラッグピーク (Bragg peak) は、ドイツ語においても “Stopping-Power” および “Bragg-Peak” と表記して用いられている。 --> |
<!-- 英語の用語であるストッピングパワー (stopping power) とブラッグピーク (Bragg peak) は、ドイツ語においても “Stopping-Power” および “Bragg-Peak” と表記して用いられている。 --> |
||
2023年8月23日 (水) 03:59時点における版
ブラッグ曲線(ブラッグきょくせん、Bragg curve)とは、アルファ線や陽子線など重荷電粒子が物質中を透過する際に示す、単位長さあたりの電離数(比電離)の変化(エネルギーの吸収量変化)を示す曲線である。1903年、イギリスの物理学者ウィリアム・ヘンリー・ブラッグ (William Henry Bragg) によって発見された。
質量の小さい荷電粒子は物質中を通過するときに散乱するが、質量が大きい重荷電粒子は散乱せずに進行(入射)方向の物質を電離しながらエネルギーを失って行く。物質中を進む重荷電粒子は運動エネルギーを失って速度が低下するに従い、速度の2乗に比例して大きな抵抗を受けるため、ある一定速度まで遅くなると急激に停止する。このとき、停止点近傍では非常に大きな電離を受け、大線量を発生する。この現象を利用するものが重粒子線療法である。
概要
高速の荷電粒子が物質内を通過するとき、その荷電粒子はその経路に沿って物質原子を電離し、イオンと電子との対を作る。入射した荷電粒子は次第にエネルギーを失って行く。 荷電粒子は物質内の経路を単位距離進むにつれてエネルギー損が増大して行き、いずれ停止する。 この荷電粒子の通過距離とエネルギー損の関係をプロットしたものを、発見者のウィリアム・ヘンリー・ブラッグに因んでブラッグ曲線 (Bragg curve) と呼ぶ。 物質内を進む荷電粒子が停止する直前、エネルギー損は最大になり、続いて急激に(ほぼ)ゼロにまで低下する。この極大部分はブラッグピーク (Bragg peak) と呼ばれる。 この現象は放射線療法において非常に実際的な重要性を有する。また、ブラッグピーク後のブラッグ曲線の接線が比電離ゼロの軸と交わる点(距離)のことを飛程という。
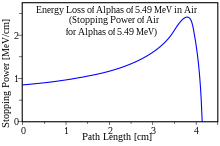
右図は単位距離ごとのエネルギー損(阻止能)を示したものである。この図でわかるように、大気中を飛行するアルファ粒子の電離密度は、その値が極大に達するまで増加し続ける。 5.49 MeVのエネルギーというのは、土壌中に花崗(かこう)岩が含まれるところであればどこにでも存在する天然ラドンガス(ラドン222)のアルファ線放出エネルギーに相当する。

二つ目の図では、粒子加速器によって発生させた250 MeVの陽子線ブラッグ曲線(赤の曲線)がどのようなエネルギー損を示すかを見て取れ、この性質がいかに放射線療法において重要性を有するかがわかる。 この250 MeVというのは、ヒト組織に適用する際、貫通深度を考慮して用いられ得るエネルギー強度である。 ブラッグピークは非常に鋭い。このことは周辺組織に大きな障害を与えることなく、腫瘍に対する照射効果が密度の濃いものになりうることを意味する。 図の青い曲線は、例えばエネルギー加速器を調節することによって、照射される腫瘍体積がより大きくなるように、ブラッグピークがどのように広げられるかを示している。 最後に、緑の曲線は根本的に赤および青の曲線とは性状が異なっている。すなわち、高エネルギーX線の吸収動態である。この曲線にはブラッグピークが見られないが、エネルギー強度は裾野の広い指数関数曲線として捉えることができる。
関連項目
